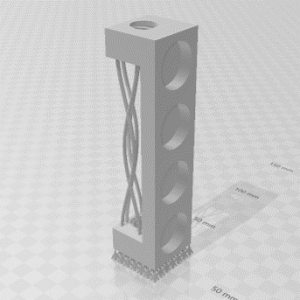
前回はテンセグリティ構造の3DデータをBlenderで作製しました。
今回はそのデータを3Dプリント用に出力し、印刷します。
【3Dプリント用に出力】
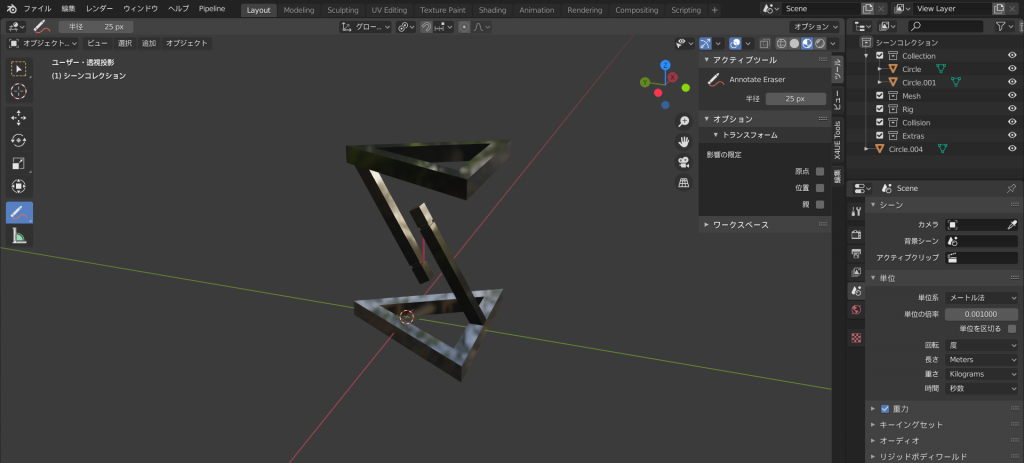
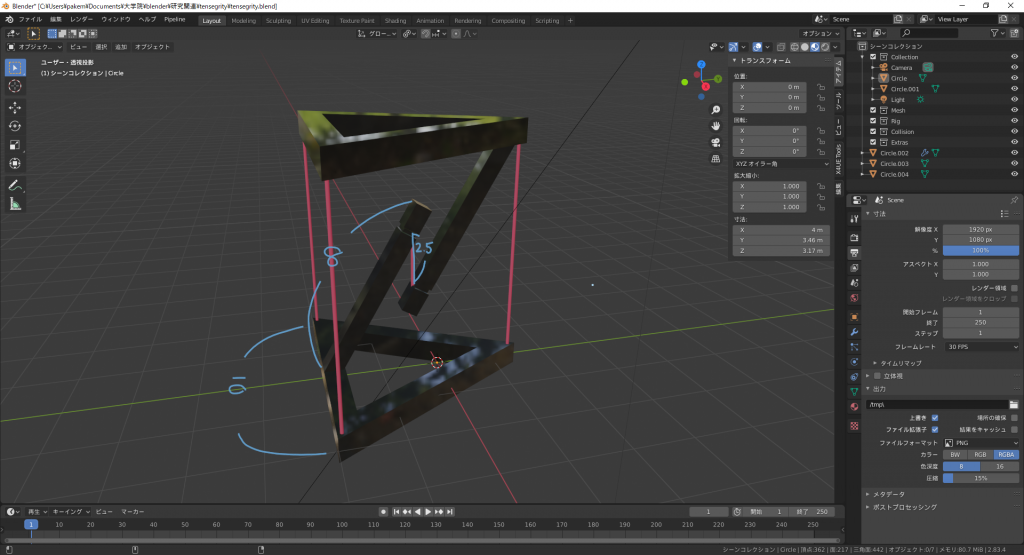
前回つくったBlenderデータはこんな感じでした
画像右下にあるように、単位はメートル法にして、単位の倍率は0.001 (1 mm)と設定します
これは印刷スケールをでかすぎず、小さすぎない大きさにするためです
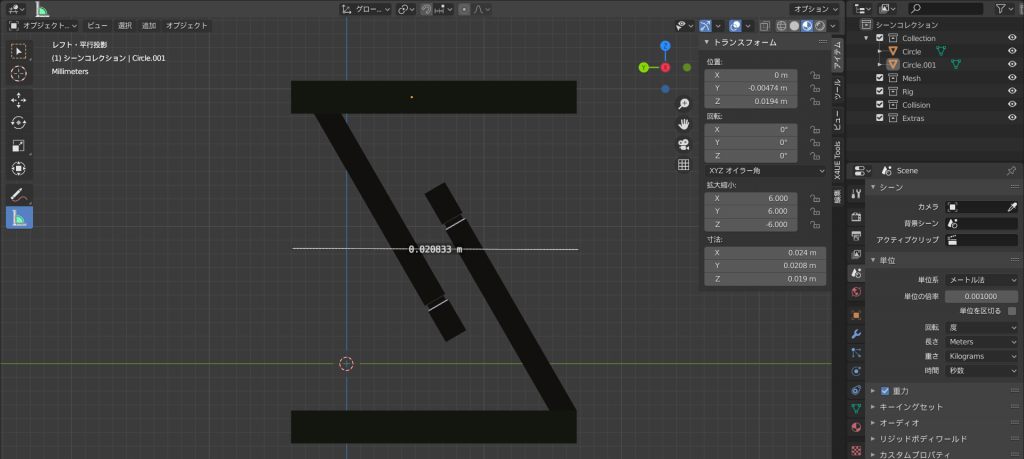
印刷物がどれくらいの大きさになりそうかは、距離を測定するツール(左から選べる)で明らかにしておきましょう
この場合は横が0.02 m (2 cm)くらいですね
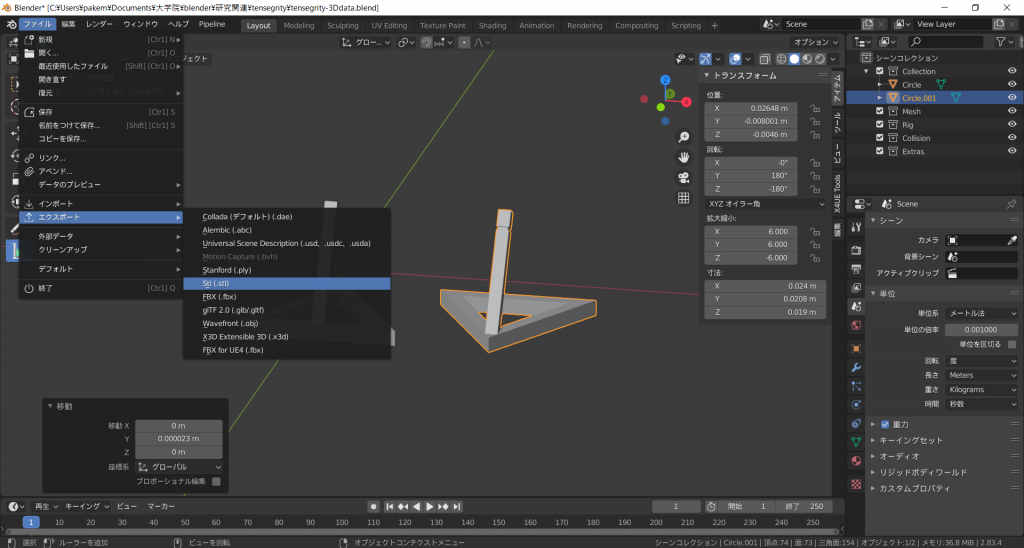
大きさが大丈夫そうなら、stl形式でエクスポートしておきましょう
この形式は3Dプリンタデータを作成するための、スライサーソフトで読み込める形式です
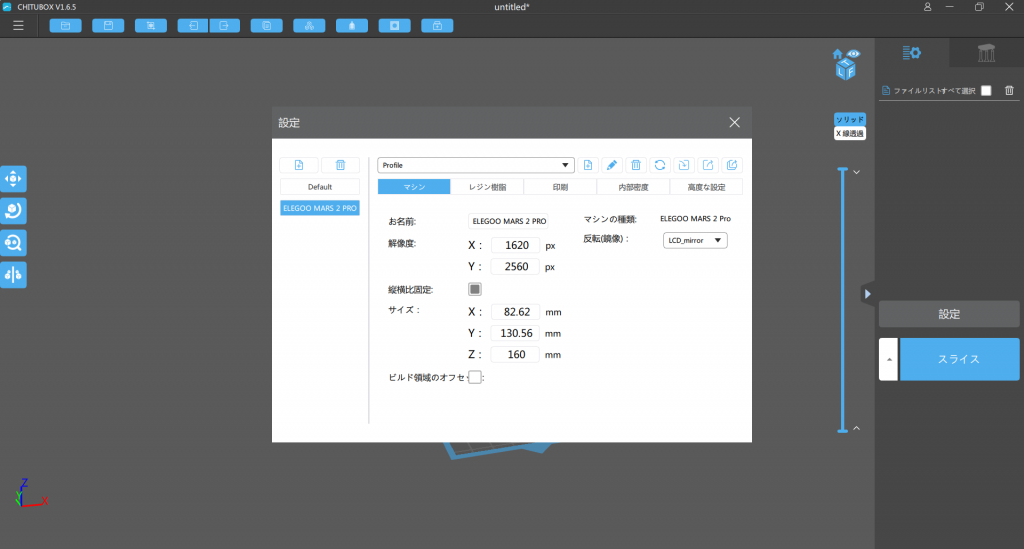
ELEGOO MARS 2 Proを購入した人は、付属のUSBにスライサーソフトであるCHITUBOXが入っています
これをインストールして起動し、右のメニューバーから設定を開いて、対応する3Dプリンターを選択しておきましょう
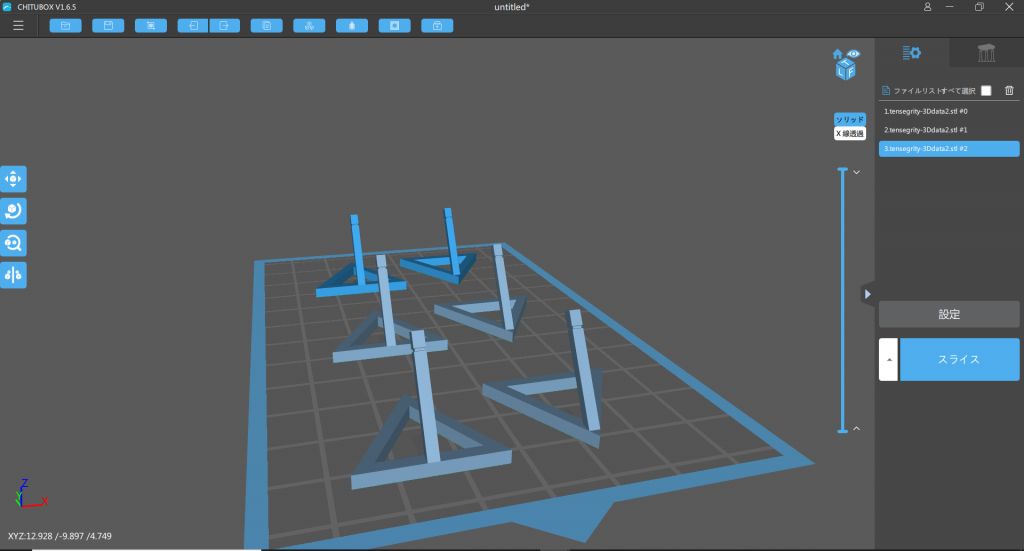
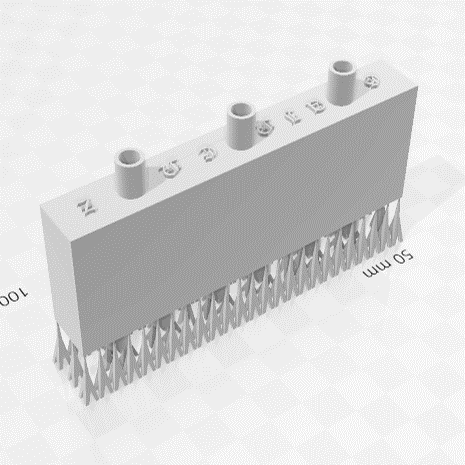
さっき保存したstlファイルを読み込むと、ビルドプラットフォームを床として、どれくらいの大きさになるかを表示してくれます
何個でも読み込めます
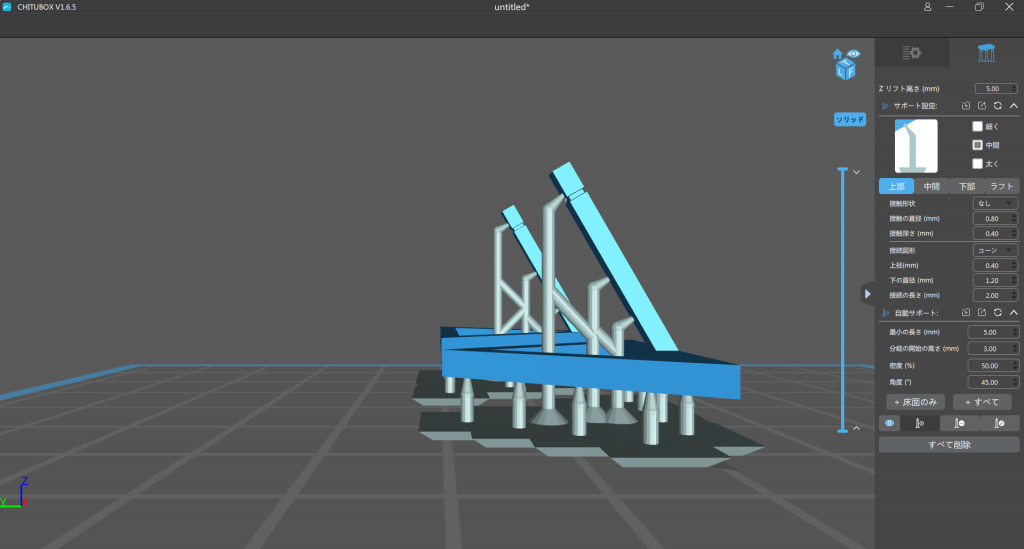
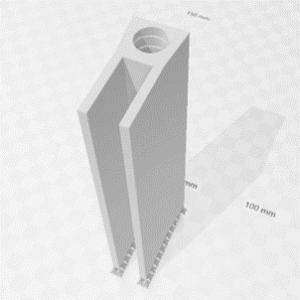
貼りだした部分は造形中に落ちてしまう可能性がありますので、このようにサポート材をつけておきましょう
サポート材のつけ方が分からない場合は、とりあえず右のメニューバーから「+すべて」を選択しておきましょう
それでも足りなさそうな箇所があれば、自分でサポート材を挿入していきます
保存したら、3Dプリンターに入れるUSBメモリのどこでもいいのでファイルを置いておきます
【実際に印刷】
キャリブレーションを行ったら、前回同様に印刷していきます

できあがっていく層が順に見えます。ワクワクですね
今回のデータは1時間くらいで印刷終了です

ビルドプラットフォームを見てみると、ちゃんとできあがっています
初めて印刷する場合はできないことも多いらしく、サポート材のつけかたを工夫しなければならないと一般には言うのですが、今回は一発で上手くいきました

ビルドプラットフォームを取り外すと、こんな感じです

ヘラをいれてとります

ペンチでサポート材から取り外します
これは二次硬化の前で大丈夫だと思います
二次硬化後だと、材料がタフすぎて切れにくいのではないでしょうか

二次硬化は10分としました

せこいですが、上下の接続部分はゴムなどをつかってつなぎとめ、完成です
中央の軸同士をとりあえずつなぎとめてから、周りの3本の糸(ゴム)を等しい長さでつなぎとめるのがポイントです
ちょっとバランスが狂うと、全然テンセグリティにならないです
まず注目すべきポイントは、中央の軸同士を結び付けるための切込みがちゃんと3Dプリントされているということです
これは定規で測ってみると、だいたい0.2 mmくらいです
素晴らしい精度ですね
そして、そんな窪みに入るような糸を探すのが大変でした
ドンキホーテまで行きましたがありませんでした
最終的にたどり着いた答えは、自分の髪の毛でした
ブリーチしてる上、めっちゃ細いのでぱっと見では分からないと思います
そして注目ポイント2つ目
浮いたような構造であるテンセグリティ構造になっています
構造的には、これは準安定状態ですね
ですので、ちょっと倒してみると、最安定状態である崩壊した構造(↓)に落ち着きます
ただし、本当に少しの力では揺れるだけで最初の準安定状態を保持します
(だから準安定状態と呼んでいます)

この挙動をグラフっぽく表してみると下のようになります

二値しかとらないということで、ロジスティック回帰で使われるようなシグモイダル関数のようになるわけです
加えて、これは推測ですが、このようにはっきりとした二状態をとれるテンセグリティ構造は、ヒモ部分がゴムであるからこそかもしえません
実際に、この記事より後のタイミングで作製した鎖型テンセグリティ構造だと、このような挙動を示していません
今回のゴム型のテンセグリティ構造の挙動は、動画にしてYoutubeにアップロードしておきます
以上、3Dプリンターでテンセグリティを作る回でした
ここまで読んでくださり、ありがとうございました。
将来的には、ヒモ部分も3Dプリントでつくった鎖で置き換えるなどして、100%3Dプリント造形物のテンセグリティをつくろうと思います
そのためにはまず、鎖を3Dプリントで作製していくこととなります