先日、このような投稿を見つけました

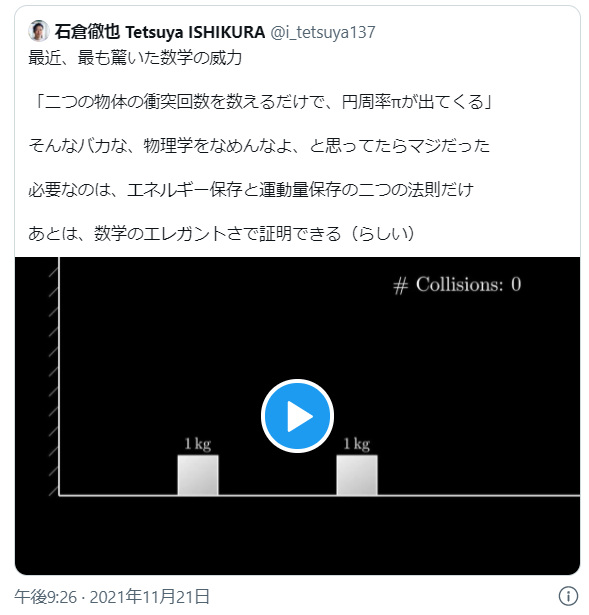
1 kgの物体に対して100のn乗 kgの物体を水平にぶつけると、壁側の物体の衝突数は314159265…となり、円周率が求められるというものです

多くの人は、このツイートのように「そんな馬鹿な」と最初に思うはずです

そこで、車輪の再発明とはなりますが、これを画像処理を用いたシミュレーションで確かめることにしました

まずはその背景となる物理を理解することにします

理解するついでに、解説することにしました

前提条件

改めて、この物理の前提条件を書きます

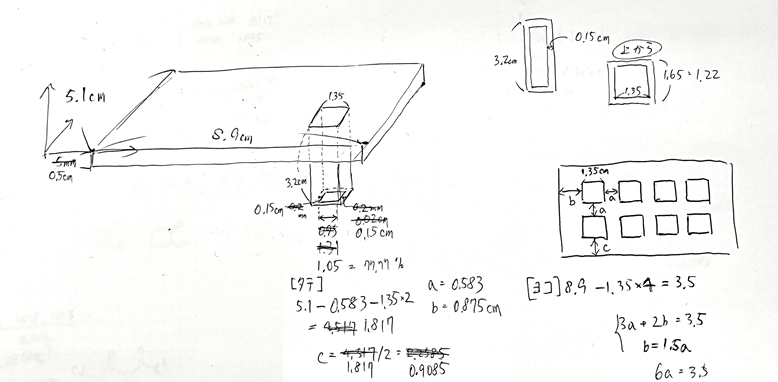
それは下の図に示す通りです

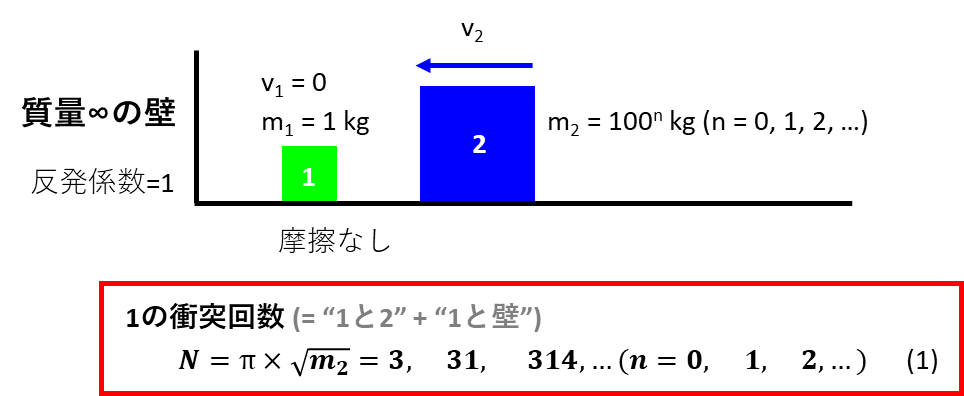
左から、質量無限の壁（動かない）、質量1 kgの物体1(緑)、質量m₂ = 100ⁿ kgの物体2(青)があります

壁は、速度vで衝突してきたものを、速度マイナスvで逆方向に返します（反発係数が１）

物体1は、最初は停止しています

一方で物体2は、摩擦ゼロの床上を左に速度v₂で向かってきており、物体1に衝突します

この衝突をプラス1として数えます

さらに、速度v₁で動き始めた物体1は壁にぶつかり、跳ね返ります

この衝突も、プラス1として数えます

この一連の動作を繰り返すと、最終的な衝突数Nは314159265…になります

実は結論から言うと、上図の赤枠内の式(1)として表したように、衝突数Nはπ×√m₂となります

このように質量m₂にはルートがついているため、質量m₂が100ⁿであることによって、最終的な衝突数は円周率3.14の10倍や100倍といったきれいな数字になってくれます

では、なぜこうなるのかを見ていきましょう

位相空間を描く

この現象を視覚的に理解するために、位相空間を描いてみましょう

位相空間とは、難しそうな名前ですが、ただのグラフです

なんのグラフかというと、今ある2つの物体の速度v₁とv₂をそれぞれヨコ軸・タテ軸に表示したグラフです

v₁とv₂の間にどのような関係式が成り立つかを考えれば、例えばy=xで直線を表すかのような描画が可能になります

今回成り立つ関係式は次の通りです

①運動エネルギー(E)保存の法則

②運動量保存(M)の法則

という2つです

これらについて、v₁とv₂を用いて具体的に表した数式は、下図ように、式(2)と式(3)になります

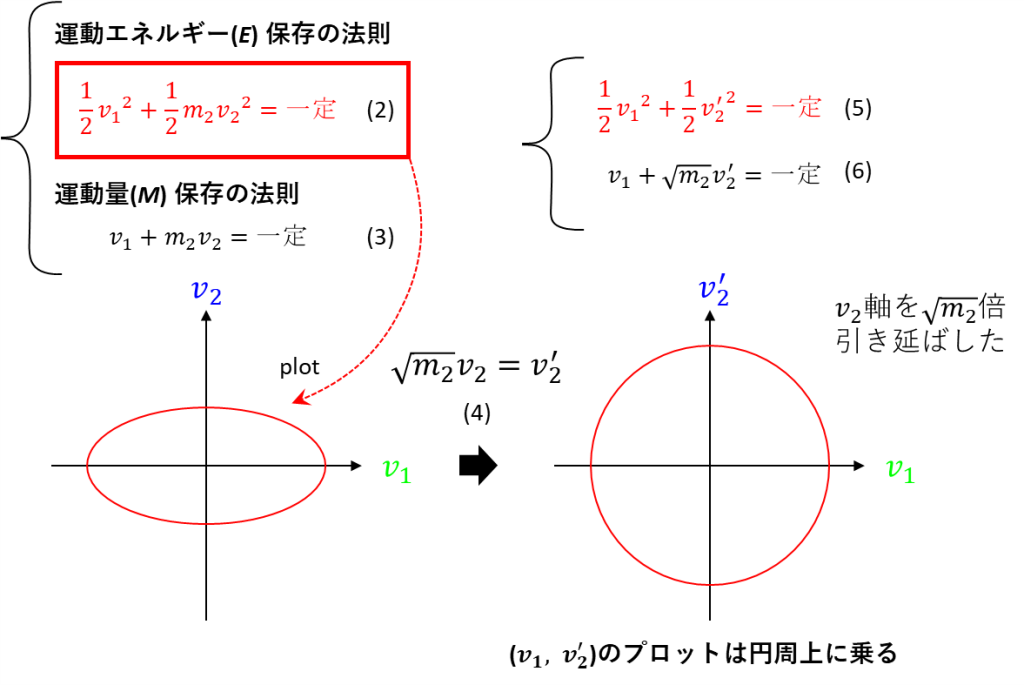
ここで式(2)を位相空間上にプロットしたものが、図の左下の楕円形となります

2つの物体の速度v₁、v₂がこの赤い楕円の円周上にある間は、エネルギーが保存されているということです

このようにエネルギー保存の法則が円形でなく楕円形となるのは、物体2が小さい速度であっても大きい質量を有しており、速度ではなく質量という形でエネルギーを貯めておけるためです

ただこの楕円は、人間にとって捉えにくい形状であるので、縦軸を√m₂倍引き延ばすことで、正円に変換しましょう

これは式(4)の式を適用することで可能です

これによって、式(2)は式(5)の形になり、「x²+y²=一定」という正円の方程式に一致します（上図の右側）

同時に、式(3)は式(6)の形になります

注意点として挙げられるのが、新たな縦軸はv₂ではなくv₂‘になっていることです

つまり、これからは(v₁, v₂)のペアではなく、(v₁, v₂‘)のペアをプロットすることになります

(v₁, v₂‘)のプロット点は、常にこの新しい正円の円周上にある、ということになります

位相空間上のプロット点の変動を考える

では、物体の衝突を考えていきます

ここでは、話を簡単にするために、物体1と物体2はどちらも質量が1 kgであるとします

1 = 100の0乗であり、n = 0の場合に相当します

まずは、物体2が速度-1で動いているとき（左をマイナスと定義）、すなわちまだ衝突数が0であるときの位相空間上のプロットを見ましょう

このときの状況を下の図の左側に示します

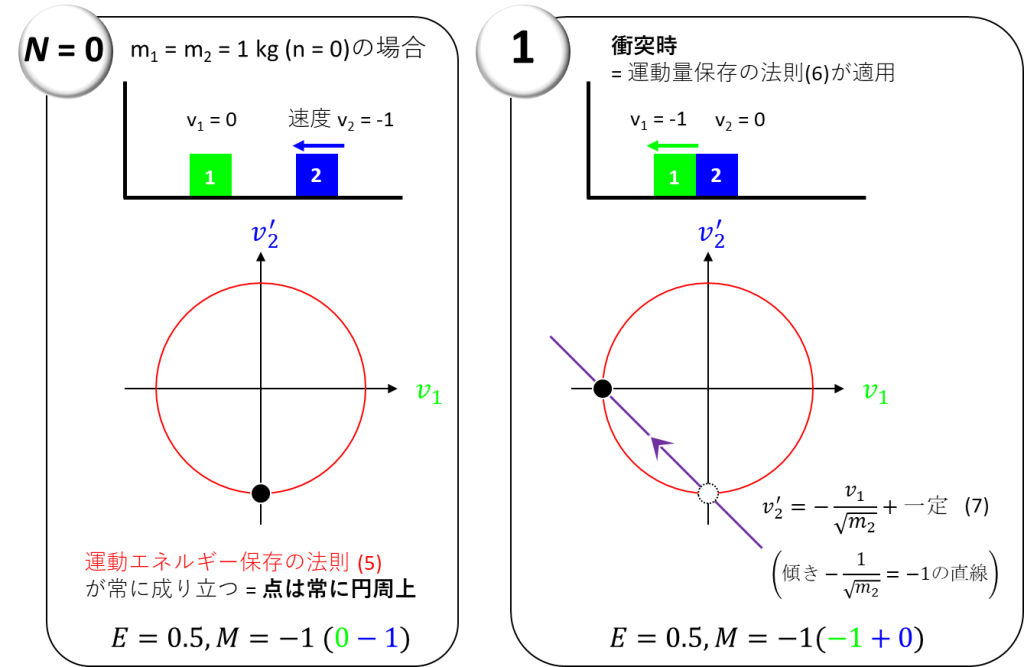
物体1は速度が0ですから、(v₁, v₂‘)のプロットは(0, -1)となり、赤い円周上の最下部にあることが確認できます

このとき、物体1と物体2のエネルギーの合計Eは、式(5)より0.5であり、このあとも一生そのままです

一方で、物体1と物体2の運動量の合計Mは、式(6)より-1であり、物体1と物体2の衝突時のみ一定値として保たれます

[衝突数N=1]

そこで、次に物体1と物体2が衝突してみたとします（上の図の右側）

衝突が起きるわけですから、(v₁, v₂‘)のペアは今までの値を捨て、それぞれ新しい値をとります

その新しい値のペアはまた赤い円周上に生じます

では、そのどこかというと、これを求めるときに運動量保存の法則を使います

運動量保存の法則を示す式(6)は、式(7)の「v₂‘ = 傾き×v₁+切片」という形に変換できるわけです

この式(7)の形は、傾きが-1/√m₂の直線に対応しています

今回のm₂ = 1という場合では、その傾きは-1になります

つまり点(0, -1)を通るこの直線と、赤い円の交点が、新しい(v₁, v₂‘)の位置となります

新しい(v₁. v₂‘)は、赤い円周上の最も左側にある点(-1, 0)です

このことは、物体2のエネルギーが完全に物体1に移り、物体2が停止する代わりに物体1が動きだすことを意味しています

[衝突数N=2]

動きはじめた物体1は、次に左の壁にぶつかり、逆向きに反発します

当然、このときもエネルギー保存の法則は一定のまま、E=0.5を保持します

しかし、この衝突は”物体1と壁”の衝突ですから、”物体1と物体2″の間にある運動量保存の法則は成り立ちません

物体1が反転することによって速度は-1から+1に変化し、これに伴って運動量の合計Mも-1から+1に変化します

この挙動は、位相空間上においては下図左のように、紫の右向きの水平線で表されます

このようにして、(v₁, v₂‘)は新しい点(1, 0)に移動するわけです

[衝突数N=3]

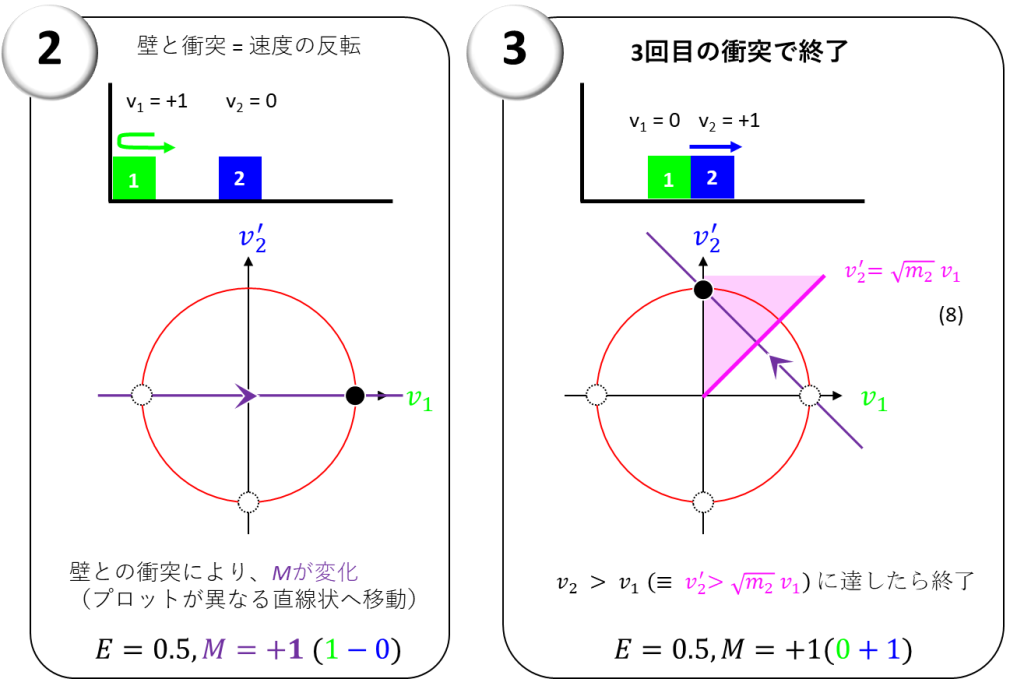
残るは、右向きになった物体1が物体2に衝突するのみです

この場合も、運動量保存の法則が成り立ちますから、 式(7)を活用することができます

この式は位相空間上において、図の右側に示した通り、(v₁, v₂‘)が一番右の(1, 0)から一番上の(0, 1)へ向かう直線に対応します

一般に、v₂ > v₁ > 0という状況になると、遅い物体1はより速い物体2に追いつきませんから、衝突は終了します

この関係はv₂‘ > √m₂ × v_1と書き換えることができ、図のピンクの領域に対応します

点(0, 1)はこのピンクの領域に収まっているので、衝突は終了ということになります

今回の衝突数の合計は3であり、これは円周率3.14の3となります

Nはπ×√m₂ ですので、m₂が100なら衝突数は31に、m₂が10000なら衝突数は314になります

位相空間の図解

位相空間上のプロットの挙動が分かったところで、Nとm₂の関係を詳しく見ていきましょう

上で示した一連の衝突は、円周上におけるプロットの変遷であり、円を分割することによって、3つの等しい大きさの円弧を生じています（下図の左）

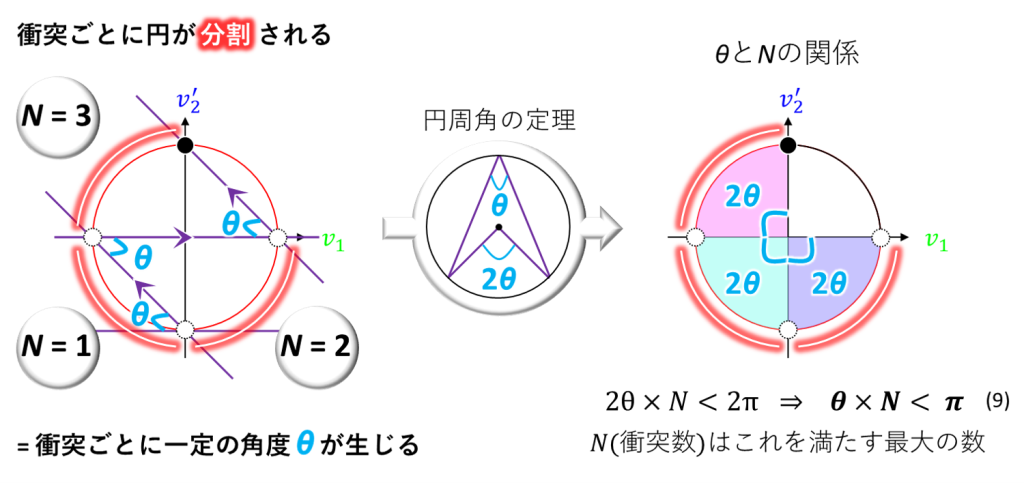
また、これらの点をつないでいくと、一回の衝突ごとに、水色で表される角度θが生成していることが確認できます

ここで、円周角の定理を用います

円周角θと対応する中心角は2θの大きさで表されるという定理ですね（上図の中央）

これを用いると、分割によって生じた3つの円弧は全て、2θの中心角を有することが分かります

ここでθとNの関係について確実に言えることは、N個ある2θを合計した角度である2θ×Nは、2π（360度）に満たないということです

これは、2θ×N < 2πと表すことができ、式(9)のようにθ×N < πと書き換えられます

この式を満たしている限り、Nはどこまでも大きくなることができます

物体1と2の質量がどちらも1 kgであるとき、図からθはπ/4であり、式(9)よりN < 4（N = 3)となることが確認できます

【補足】

上の図を見ると、 2θ×N = 3π/4と思われる方もいらっしゃるかもしれません

たしかに、1 kg vs. 1 kgという今回の場合ではそうですが、一般的ではありません

試しに、N = 4まで衝突が起きる場合を考えてみてください

この場合は、第一象限にある円周上にもう一つのプロット点が増えます

すると、第一象限の円周も分割され、新たなθを生じるわけです

このとき2θ×N は3π/4を超えており、2θ×N = 3π/4 はもはや満たされないことが分かると思います

したがって、いつも確実に言える一般事象は、 θ×N < π ということになります

θと物体2の質量の関係

では、急に出てきたθとは、物理的にはどんな意味をもつのでしょうか

物体2の質量m₂とどのような関係があるのでしょうか

これは下の図から明らかにすることができます

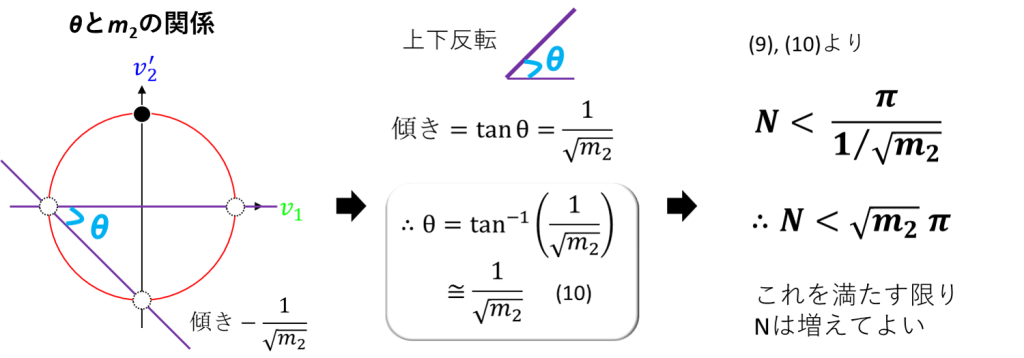
θとは、式(7)と横軸の間の角度です

ここで、式(7)は傾きが-1/√m₂の直線です

図のθを形成する2つの直線を上下反転させてみると、この傾きは+1/√m₂に対応します

さらに、この傾きはtanθです

つまり、tanθ = 1/√m₂がなりたちます

これをθについて解くと、θ = arctan(1/√m₂)と表すことができます

一般に、εが小さいとき、arctan(ε) = εとして近似してよいことになっています

このため、さらにθはθ = 1/√m₂ …式(10)として書き換えることができるわけです

Nと物体2の質量の関係

式(9)より、Nとθの関係がわかりました

また式(10)より、θとm₂の関係が分かりました

ということは、これらを組み合わせれば、Nとm_2の関係が分かりますね

これが、上の図の右側で表したように、N < √m₂ × πとなるわけです

m₂が100 kgなら √m₂×π は31.415…であり、Nはこれを満たすまで増えてよいのです

したがって、衝突数は円周率の10倍や100倍に対応しており、m₂が大きいほどに、その精度は向上します

これで、この衝突の物理を理解することができました

次回は、これをProcessingを用いた画像処理でシミュレーションします

読んでいただきありがとうございました。