4 6月 2022

【Blender】ノードプログラミングで色を変える方法

by GAINENZ | posted in: 3D Modeling, Processing, Technology | 0

本記事で解説するのは、以下のようなテクスチャの部分的な変更をノードプログラミングで行う方法です

（動画バージョンもあります！）

かわいいクアッカワラビーですね

このクアッカワラビーは、REVOPOINTで3Dスキャンしたオブジェクトに対し、テクスチャを設定したものです

元々のテクスチャは以下のように設定されています

今回は、この上の図の↘で示された色のみをピンクに変える方法を解説します

指針：変えたい部分を1にし、1を好きな色に変える

指針としては、これが全てです

上で示した↘の色部分を1にします

1というのは、こういう画像処理的な場面においては白だと思ってください

反対に、0は黒を意味します

なぜ1にするかというと、1に”何か”を掛け算すれば、そのままその”何か”になってくれるからです

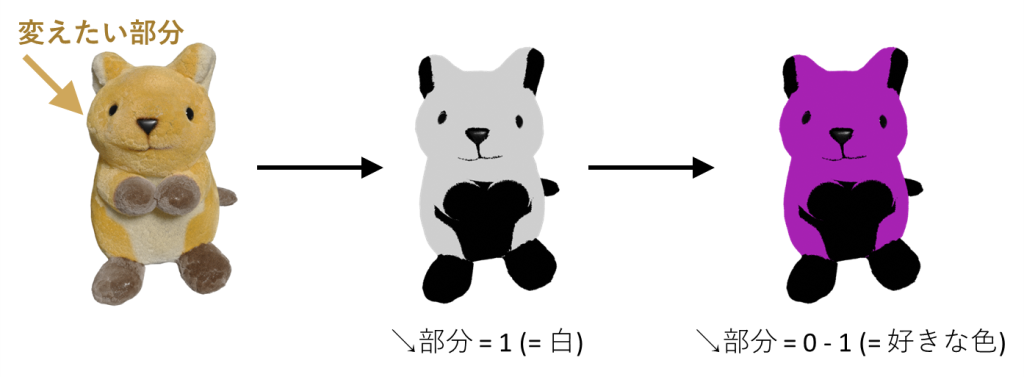
というわけで、1はすごく扱いやすい数であるため、変えたい部分を1にします

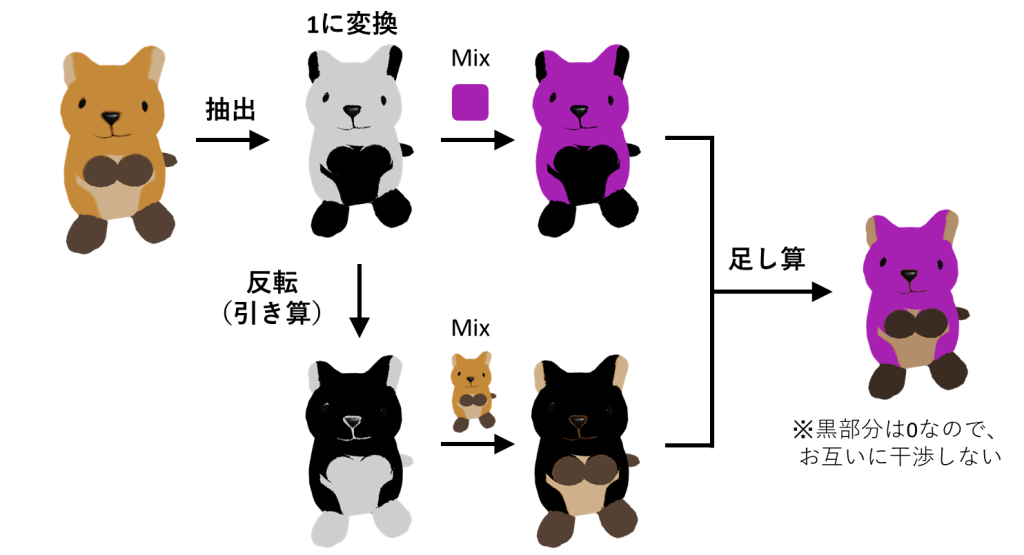
さらなる全体像は上に示しました

抽出したテクスチャは例えばピンクとMixすることによって、好きな色に変えます

そしてその対の存在となるクアッカワラビーを、抽出テクスチャを反転させることによって作製します

最後はこれらを足し算することで、一部のテクスチャのみが変更されたクアッカワラビーとします

どうやって1として抽出するか

変えたい部分を1として抽出するには、変えたい部分の特徴を知ることが必要です

例えば、その明るさに着目してみましょう

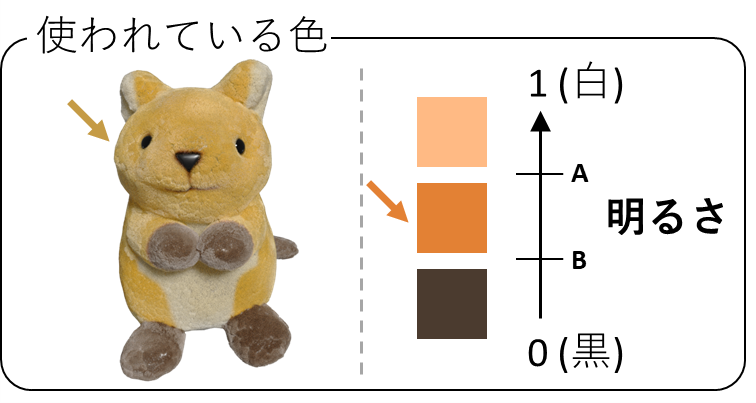
上図のように、使われている色を並べてみると、変えたい部分は中間程度の明るさを有していることがわかります

これも一つの特徴です

そこで、まずある明るさ(A)以下のテクスチャを抽出すると、下図左のようになります

加えて、ある明るさ(B)以上のテクスチャを抽出すると、下図中央のようになります

ほしいテクスチャは、この両方のテクスチャの共通部分ですから、これらに対して掛け算を行います

つまり、積集合を得るというわけです

これによって、明るさが中間程度となっている部分のテクスチャを選択的に1にすることができます

具体的なノードプログラミング

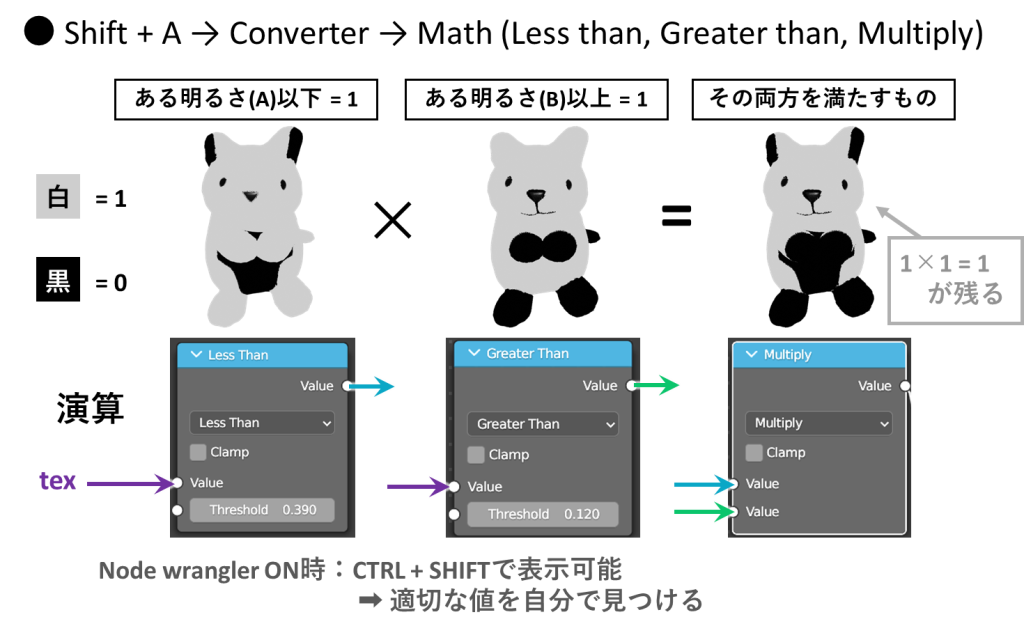
上述した掛け算を具体的にノードプログラミングで行う方法は、上図の通りです

ある明るさ”以下”と”以上”は、それぞれ”Less than”と”Greater than”という演算で得ることが出来ます

これらのノードをさらに”multiply”というノードにつなぐことで掛け算が行われ、1×1=1という演算に対応する部分が出力されます

1に任意のテクスチャを”Mix”する

Mixは混ぜるという意味ですが、BlenderではMixというノードのことを指します

基本的な使い方は下の通りです

例えば図の左側のように、係数(fac)が0であれば、Color1だけが出力されます

係数が1であればColor2だけが出力され、係数がその間なら、その係数に従った比で混合された色が出力されます

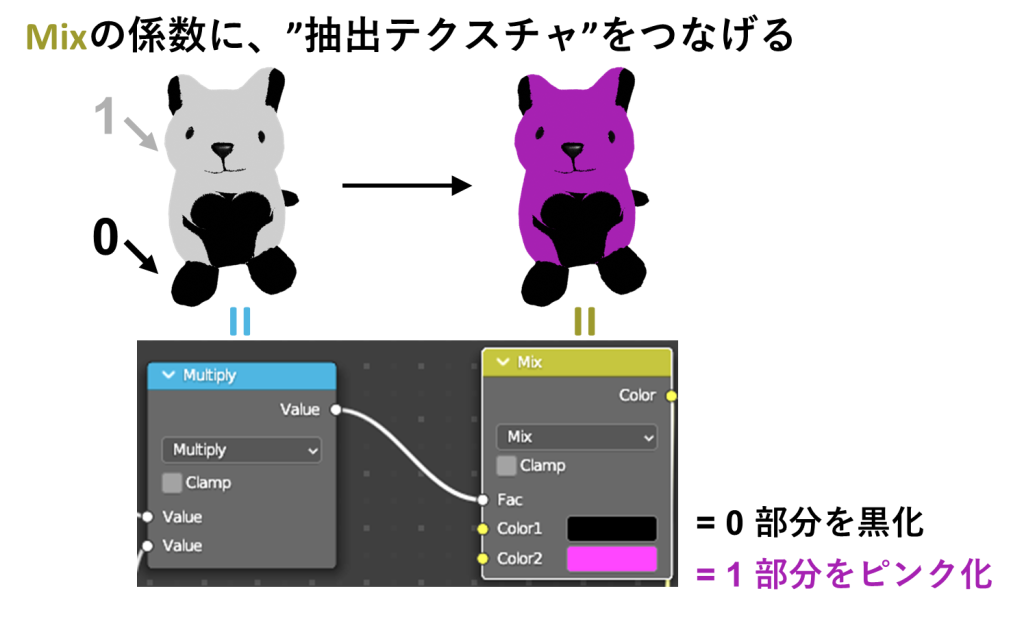
そこで、今度はMixの係数に、先ほどまでに作成した”Multiply”のノードをつなげてみましょう

このようなノードを組むと、テクスチャの抽出部分(= 1)に対してはColor2を適用でき、テクスチャの非抽出部分(= 0)にはColor1を選択的に適用できます

これによって、抽出部分だけ好きな色に変えることができるわけです

抽出テクスチャの反転と、元のテクスチャとのMix

0と1で構成されたテクスチャを反転するには、「1から引く」という操作を行えばよいです

これは下図に示しました

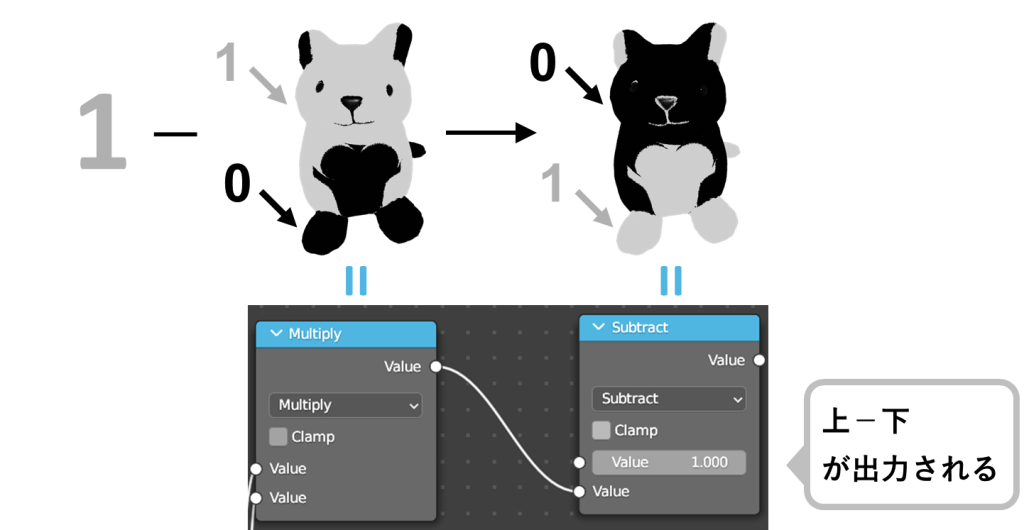
このような操作を行うことで、画像のように、元々1であった部分は0となり、元々0であった部分は1となります

これはノードプログラミングにおいてはMathのSubtractをつなげることによって出力できます

さらに得られた反転テクスチャに対しては、Mixノードを用いることで元のテクスチャを反映されましょう

やり方は下の画像の通りです

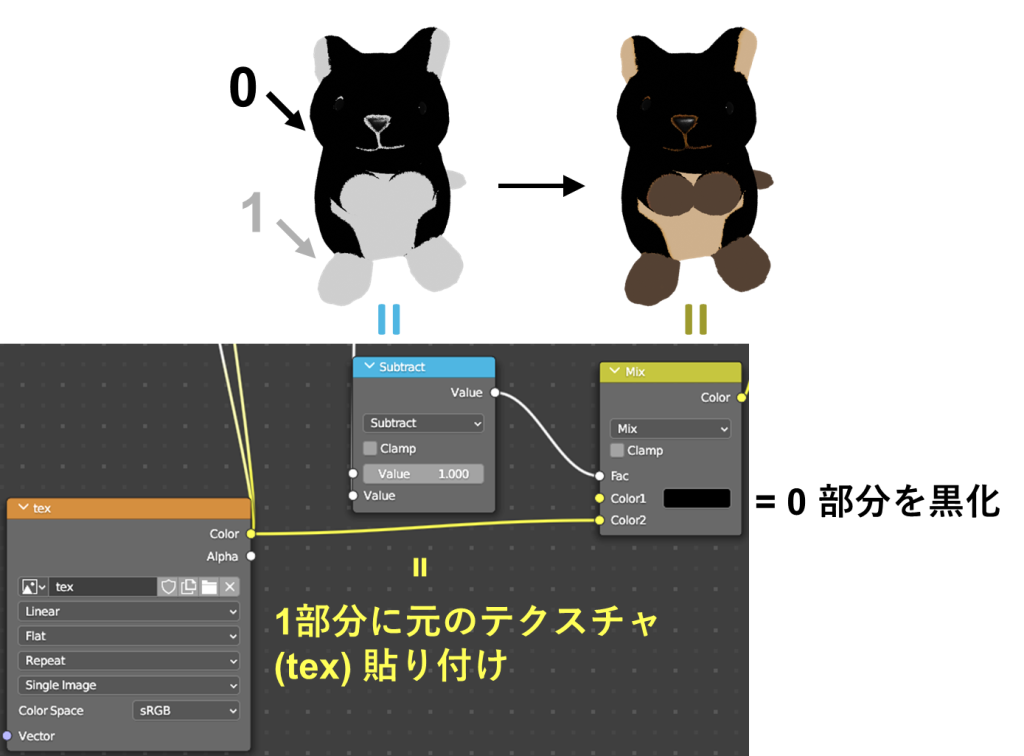
係数には反転テクスチャ(Subtractの出力)をつなげ、Color1には黒を、Color2には元のテクスチャをつなげましょう

ここで得られるテクスチャが、先ほどピンクになったクアッカワラビーと対の存在になります

最後は足すだけ

ここまでで、一部がピンクになったクアッカワラビーとその対になるクアッカワラビーを作製してきました

最後はこれらを足すことによって、一部だけ色の変わったクアッカワラビーを出力できます

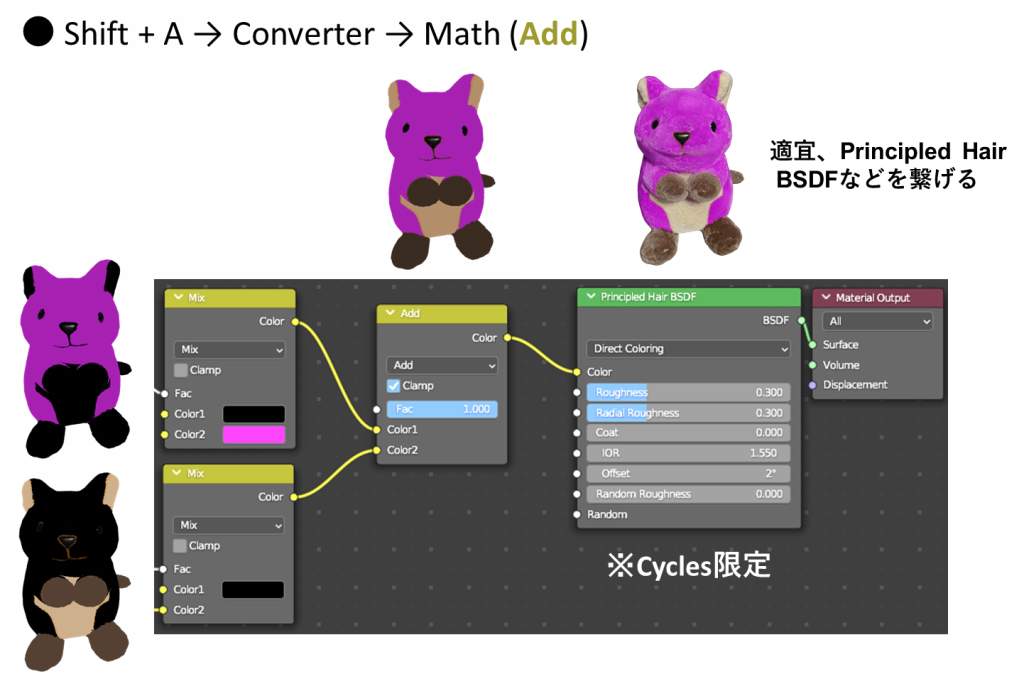
加算(Add)という演算はMathノードのプルダウンメニューから選択することができます

このAddのColor1とColor2に、これまで作ってきた2つのMixノードをつなげましょう

最後に、このAddの出力となるColorを何かしらのBSDFにつなげれば、テクスチャの質感を制御できます

操作は以上で終了です

まとめ：ノードの全体像

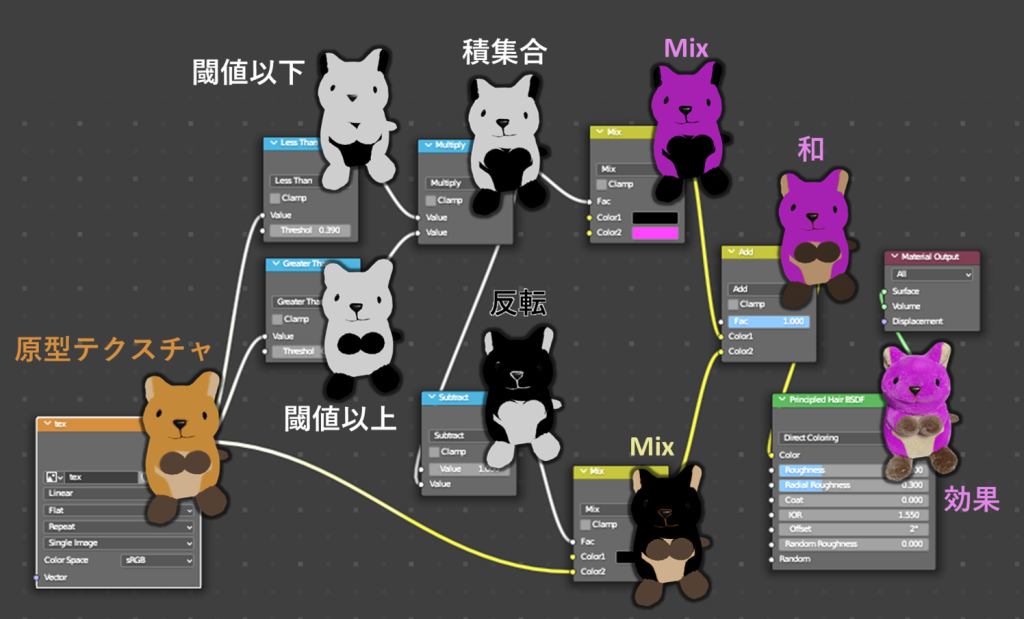
最後に、こちらに上述した操作のまとめをお示しします

原型テクスチャを途中で分岐させて、後半の段階でまた統合していることが一目瞭然であると思います

また、今回のこの解説については動画でも行っています

ノードプログラミングの基礎を知りたい方、ぜひご覧ください！

21 5月 2022

3Dプリンターの光源スペクトルと光開始剤の選定

by GAINENZ | posted in: 3D Printing, Chemistry, Technology | 0

一般に光造形型の3Dプリンターは405 nmの光源を搭載しています

405 nmが何を指しているかと言うと、紫〜青色光のことを意味しています

（光は電磁波であり、400 nm程度の波長であれば紫〜青色光に、800 nm程度の波長であれば赤色光に対応しているということは知っておくと良いでしょう）

つまり、光造形型の3Dプリンターは405 nmという青色光をレジンに照射することによって反応を引き起こし、造形を行っているわけです

ここで、ある3Dプリンターの光源のスペクトルを以下に示します

（このスペクトルは、私が実際に3Dプリンターの光源のスペクトル測定を行うことによって得た光源スペクトルから、それとほぼ同じ形状となるように描きなおしたものです）

このスペクトルにおいて横軸は波長を意味しており、縦軸は強度（または分布）を意味しています

ですので、この光源スペクトルに着目すると、3Dプリンターは405 nmの光に加えて、大体390から430 nmの光もわずかに含んでいるということが分かります

光化学第一法則

光化学第一法則は、「Grotthuss–Draper law」という名前でも知られています

この法則は、「吸収された光だけが、化学反応を起こすことができる」という法則です

裏返して言えば、「光が吸収されなければ、化学反応が起こることはない」ということになります

ここで3Dプリンターの話に戻ります

先ほど、3Dプリンターは390-430 nmの光を含んでいると述べました

ですので、390-430 nmの光を吸収するような光開始剤であれば、化学反応を引き起こすことでレジンを硬化させることができます

このような光開始剤は青色光を吸収するわけですから、見た目としては黄色を呈していることになります

一方、例えば250-330 nmの光しか吸収しないような光開始剤があったならば、それは一般的な3Dプリンターではレジンの硬化を引き起こせないということになります

以下には、適切な光開始剤の吸収スペクトルを、3Dプリンターの発光スペクトルとともに示します（縦軸の強度は適当です）

上図の例では、BAPOという光開始剤の吸収スペクトルを紫色で表示しています

この吸収スペクトルは、光の長波長化に従って吸収能力が低下することを示しているものの、3Dプリンターの光源スペクトルとの間に重なりを有しています

したがって、BAPOという光開始剤は、405 nm光源を有する3Dプリンターで化学反応を開始させられるということが分かります

光開始剤といっても、BAPOだけとは限らず、多様なものが知られています

そこで本記事では、以下に光開始剤の種類と、その吸収能力が最も高くなる波長（λ_max）範囲についてまとめました^[1]

光開始剤を選定する場合は、用いる光源のピークトップに対応する波長が、可能な限り光開始剤のλ_maxと適合することを心がけましょう

1: Benzophenone, 2: Phenyl bis (2,4,5-trimethylbenzoyl) phosphine oxide (BAPO, Irgacure 819), 3: 2-hydroxy-2-methyl-1-phenyl-propan-1-one (Irgacure 1173), 4: 2-hydroxy-4′-(2-hydroxyethoxy)-2-methylpropiophenone (Irgacure 2959), 5: 2,2′-azobis[2-methyl-n-(2-hydroxyethyl) propionamide] (VA-086), 6: 2,2-dimethoxy-2-phenylacetophenone (Irgacure 651 or DMPA), 7: Diphenyl(2,4,6-trimethylbenzoyl)phosphine oxide (Darocur TPO or Lucirin TPO), 8: Lithium phenyl(2,4,6-trimethylbenzoyl)phosphinate (LAP), 9: Ethyl (2,4,6-trimethylbenzoyl)phenylphosphinate (Lucirin TPO-L).

光開始剤の吸収スペクトルの詳細が気になる方は、以下のSigma aldrichのページなどが参考になると思われます

Photoinitiators – Sigma-Aldrich

特定の化合物のスペクトルを知りたい場合は「化合物の英名 absorbance」というキーワードで検索してみましょう

参考文献

[1] A. Bagheri, J, Jin ACS Appl. Polym. Mater. 2019, 1, 593.

24 4月 2022

S-S curveとMooney-Rivlin解析（理論編）

by GAINENZ | posted in: Chemistry, Computational Science, Technology | 1

S-S curveという業界用語があります

これは、物体にかかる歪み(strain)と応力(stress)の関係を表した曲線(curve)のことです

物体とは、金属・セラミクス・ゴムなど何でも良いです

ただ、S-S curveの関係がよく知られている物体を挙げるとすれば、それはおそらくバネです

なぜなら、義務教育である中学の理科で、バネの伸び(=歪み)と力(=応力)の関係を習うからです

当然ですが、バネは伸びるほど、より大きな力を発生しますよね

これは式で表すと、F = kxということになります(F: 力、k: バネ定数、x: 伸び)

このことは、バネに限れば、S-S curve(F-x curve)はきれいな直線形になることを表しています

しかしながら、一般には物体のStress-Strain関係はF = kxのような比例関係になるとは限りません

例えば、理想的なゴムであれば、

σ = G (λ – λ^-2) (式1)

という式に従います(σ:応力、G: 弾性率、λ:伸長比)

Gは貯蔵弾性率という名前でも知られていますが、その本質はバネ定数と同じであり、値が大きいほど物体が固いことを表します

固さの指標としてはヤング率Eが用いられることもあり、一般にはE = 2(1+μ) G ≃ 3Gという関係性が成り立ちます(μはポアソン比)

さらに重要なこととして、式(1)をλで微分すれば分かることなのですが、ヤング率はS-S curveの原点位置における接線の傾きと等しいです

なぜゴムのS-S curveが式(1)の代わりに、”σ = G λ”や”σ = E λ / 3″という簡単な式にならないかというと、ゴム材料はx軸方向に伸びる時、それ以外のy軸とz軸方向には収縮を起こしているためです

つまり、このような体積保存の仮定を置くと、式(1)のような少し複雑な式が導出されます(詳しくはまたどこかで取り扱います)

加えて、実は式(1)の形では、ゴム中の高分子鎖が理想的な振る舞いをするという仮定が入っており、現実の挙動からは逸脱しています

これを補正するために用いられるのが、以下のMooney-Rivlinの式です

σ = 2C₁ (λ – λ^-2) + 2C₂ (λ – λ^-2) / λ (式2)

ここで、係数C₁は主に架橋密度に関するパラメータであり、C₂は非理想性を表すパラメータです

架橋密度とは、網目の分岐点の密度のことで、この値が高いほどにヤング率は大きい（材料が固い）です

また理想性とは、ゴム内部の分子の網目が均一であることを指す言葉であり、反対に非理想性とは、網目が不均一であることを指します

例えば係数C₂が0であれば、網目の絡み合いなどといった非理想性がゼロであることを意味しており、このとき式(2)は式(1)と等しくなります

現実には網目はそう簡単に理想的にはなりませんから、中では絡み合いを生じており、この度合が高い（C₂が高い）ほどヤング率は大きいです

以上を簡単にまとめます

係数C₁とC₂、どちらの値が大きくなってもヤング率Eは大きくなる

ということです

（厳密には、E = 6 (C₁ + C₂)という式が成り立っています）

もし、式(2)が簡単な形であったなら、C₁とC₂の値がそれぞれいくつのときにどのようなS-S curveが描かれるかを頭の中でシミュレーションできそうです

しかし現実には、式(2)をイメージすることは難しいですよね

そこで今回、式(2)を直感的に把握できるProcessingスクリプトを開発しました

それがこちらです↓

S-S curveとMooney-Rivlin解析（実践編）

本ページでは、C₁とC₂の値を「+ボタン」と「-ボタン」で自由に調節することで、自在にS-S curveを描くことができます

これによって、C₁・C₂というパラメータとS-S curveの関係を直感的に把握することが可能となります

本ページのS-S curveの下に示したのはMooney rivlin plotで、以下の式(3)の左辺を縦軸に、1/λを横軸にとったものです

σ / (λ – λ^-2) = 2C₁ + 2C₂ / λ (式3)

このMooney rivlin plot上では、C₂がグラフの傾きに対応しており、C₁が切片に対応します

S-S curveとMooney rivlin plotの対応関係をぜひご覧ください

質問あれば、ぜひコメントへよろしくお願いいたします。

5 4月 2022

共重合反応の確率シミュレーション（結果・考察編）

by GAINENZ | posted in: Chemistry, Computational Science | 0

３．シミュレーションの視覚化と結果・考察

　アルゴリズム編に記載したプログラムをR Studioで実行することで、様々なBの割合においてAがBABに変換される割合、すなわち確率をシミュレーションした。

　設定したプログラムによって適切にシミュレーションが進行することについては、print()関数で確かめることができた。入力内容と出力結果のそれぞれの一部を図7に示した。図7aでは、初期の反応容器内にある分子として3つのＡと6つのBを定義している。その結果、一段階目の反応においては、6番目のBと2番目のAが選択されることでBAが生成され、flaskの最後尾に追加されることが確認できた(図7b上段)。

図7. R scriptのa)入力内容の一部とb)出力結果の一部．赤枠で囲まれた文字は一段階目の反応物と生成物を意味し、青枠で囲まれた文字は二段階目の反応物と生成物を意味する．定義は次の通りである．Turn X: X段階目、Selected index: 選択されたインデックス、All_ends: 反応分子の全ての末端、different: 選択された分子の末端が反応可能．1st-(2nd-)reactive-end: 1個目(2個目)の反応末端（左末端は1、右末端は2）、Remaining X: Xの残りの数．

さらに、二段階目では5番目のBと8番目となったBAが選択され、生成したBABが追加されることが確認できた(図7b下段)。したがって、記述したプログラムが適切に動作していることが確認できた。

　続いては分子の総数を増やし、より現実的なシミュレーションを行った。実際の化学反応において分子は1 mol (10²⁴個)程度存在するが、計算を終了させるため、分子の総数は5000個とした。反応開始時点でのBの割合を0.1、0.52、0.9とした場合に、最終的に生成した分子(文字)の長さに対する分布を図8に示した。図8では、Aから始まる分子(A…)は赤、Bから始まる分子(B…)は青、BABは紫の実線で表示している。図8aより、Bの割合が0.1と低い場合、生成物の長さは比較的短く、かつBABを生じていないことが分かる。これは、無作為抽出によってAが選ばれやすく、分子の両端に対して連続的にAが結合する確率が高かったためであると考えられる。図8bより、Bの割合が0.52の場合は、わずかにBABを生じるものの、それよりも長い分子を数多く生じていることが分かる。これは、AとBの数が同程度であることによって、どちらも無作為抽出で選ばれやすく、ABABAB…と分子が交互に伸長する確率が高くなったためであると考えられる。図8cより、Bの割合が0.9と高い場合は、生成物としてはBABを最も生じていることが分かる。これは図8aのAがBに置き換わった場合に相当しており、分子の両端が連続的にBと衝突する確率が高いことで、生成したBABはそれ以降の反応を起こしにくかったためであると考えられる。

図8. Bの割合がa) 0.1、b) 0.52、c) 0.9とした場合に生じた分子の長さの分布．横軸は分子の長さを示しており、縦軸は頻度の対数表示である．

　様々なBの割合に対して、反応したAのうちBABとなったものの割合を実験的に得られた確率値として図9に示した。図9aに着目すると、Bの割合が0.5以下である場合には、全くBABを生じないことが分かる。一方、Bの割合が0.5以上となると、BABを生じる割合が単調に増加することが明らかとなった。特に、Bの割合が0.96、0.98である場合には、BABの生成確率がそれぞれ約85%、約90%となった。したがって、Bの割合を最小限にしつつもBABの生成効率を高めるには、Bの割合が少なくとも0.96から0.98程度必要であることを明らかにできた。

図9. 様々なBの割合においてAがBABに変換された割合、すなわち確率の箱ひげ図．Bの割合がa) 0から1までを0.02ごととb) 0.98から1までを0.002ごとの場合を示す．

　興味深いことに、図9bより、Bの割合が0.98以上となる場合は、Bの割合を高めてもBABの生成確率が増大しにくくなることが分かった。これは、Bの割合が高すぎる場合には、B同士が選ばれてしまう状況が長く続き、未反応状態が続くことを抑制するwhile文によって反応が止められてしまったためであると考えられる。すなわち、AやABが存在しているにも関わらず、BABを生成する前に反応が止まってしまったため、0.998という高いBの割合であってもBABの生成確率が0となるようなケースを生じたと考えられる。このような挙動は現実の化学反応では起きず、無作為抽出を用いたシミュレーションならではのものである。現状として、計算速度を短縮させるために未反応状態の上限を1000回と設定しているため、この上限を増やすことで、さらに現実に近いシミュレーションを実現することができる。

４．結論

　本記事では、分子A,Bが交互に伸長する反応のシミュレーションを行うことで、AとBの比によって異なるBABの生成確率を系統的に調査した。その結果、Bの割合が高いほどBABの生成確率が高くなるという、現実に見られる傾向を再現することができた。特に、少ないBであっても高い確率でBABを得るには、Bの割合が96から98%程度必要であることが分かった。これによって、莫大な数の化学実験を行わずに、最適なBの割合を明らかにすることができた。