S-S curveという業界用語があります
これは、物体にかかる歪み(strain)と応力(stress)の関係を表した曲線(curve)のことです
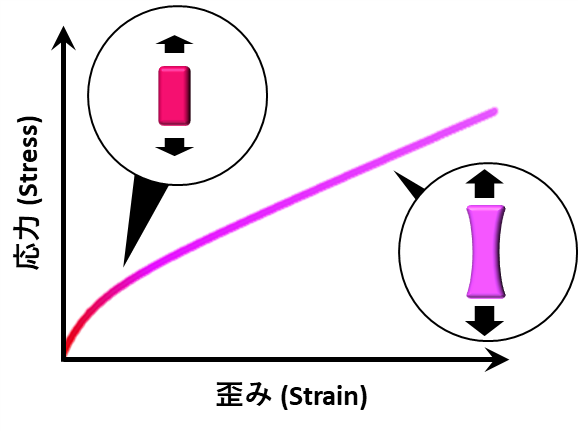
物体とは、金属・セラミクス・ゴムなど何でも良いです
ただ、S-S curveの関係がよく知られている物体を挙げるとすれば、それはおそらくバネです
なぜなら、義務教育である中学の理科で、バネの伸び(=歪み)と力(=応力)の関係を習うからです
当然ですが、バネは伸びるほど、より大きな力を発生しますよね
これは式で表すと、F = kxということになります(F: 力、k: バネ定数、x: 伸び)
このことは、バネに限れば、S-S curve(F-x curve)はきれいな直線形になることを表しています
しかしながら、一般には物体のStress-Strain関係はF = kxのような比例関係になるとは限りません
例えば、理想的なゴムであれば、
σ = G (λ – λ-2) (式1)
という式に従います(σ:応力、G: 弾性率、λ:伸長比)
Gは貯蔵弾性率という名前でも知られていますが、その本質はバネ定数と同じであり、値が大きいほど物体が固いことを表します
固さの指標としてはヤング率Eが用いられることもあり、一般にはE = 2(1+μ) G ≃ 3Gという関係性が成り立ちます(μはポアソン比)
さらに重要なこととして、式(1)をλで微分すれば分かることなのですが、ヤング率はS-S curveの原点位置における接線の傾きと等しいです
なぜゴムのS-S curveが式(1)の代わりに、”σ = G λ”や”σ = E λ / 3″という簡単な式にならないかというと、ゴム材料はx軸方向に伸びる時、それ以外のy軸とz軸方向には収縮を起こしているためです
つまり、このような体積保存の仮定を置くと、式(1)のような少し複雑な式が導出されます(詳しくはまたどこかで取り扱います)
加えて、実は式(1)の形では、ゴム中の高分子鎖が理想的な振る舞いをするという仮定が入っており、現実の挙動からは逸脱しています
これを補正するために用いられるのが、以下のMooney-Rivlinの式です
σ = 2C1 (λ – λ-2) + 2C2 (λ – λ-2) / λ (式2)
ここで、係数C1は主に架橋密度に関するパラメータであり、C2は非理想性を表すパラメータです
架橋密度とは、網目の分岐点の密度のことで、この値が高いほどにヤング率は大きい(材料が固い)です
また理想性とは、ゴム内部の分子の網目が均一であることを指す言葉であり、反対に非理想性とは、網目が不均一であることを指します
例えば係数C2が0であれば、網目の絡み合いなどといった非理想性がゼロであることを意味しており、このとき式(2)は式(1)と等しくなります
現実には網目はそう簡単に理想的にはなりませんから、中では絡み合いを生じており、この度合が高い(C2が高い)ほどヤング率は大きいです
以上を簡単にまとめます
係数C1とC2、どちらの値が大きくなってもヤング率Eは大きくなる
ということです
(厳密には、E = 6 (C1 + C2)という式が成り立っています)
もし、式(2)が簡単な形であったなら、C1とC2の値がそれぞれいくつのときにどのようなS-S curveが描かれるかを頭の中でシミュレーションできそうです
しかし現実には、式(2)をイメージすることは難しいですよね
そこで今回、式(2)を直感的に把握できるProcessingスクリプトを開発しました
それがこちらです↓
本ページでは、C1とC2の値を「+ボタン」と「-ボタン」で自由に調節することで、自在にS-S curveを描くことができます
これによって、C1・C2というパラメータとS-S curveの関係を直感的に把握することが可能となります
本ページのS-S curveの下に示したのはMooney rivlin plotで、以下の式(3)の左辺を縦軸に、1/λを横軸にとったものです
σ / (λ – λ-2) = 2C1 + 2C2 / λ (式3)
このMooney rivlin plot上では、C2がグラフの傾きに対応しており、C1が切片に対応します
S-S curveとMooney rivlin plotの対応関係をぜひご覧ください
質問あれば、ぜひコメントへよろしくお願いいたします。









romantik69.co.il
Excellent post. I definitely appreciate this website. Thanks!