Blenderで数学教材

　先日、ツイッターで下のような数学教材を見つけました

図には、黒い二次関数曲線(y=x^2+1+ax)と赤い一次関数曲線(y=c|x|)が示されています

(ここでaとcは任意の実数です)

それらは、あるx座標で接点を形成しています

そして、この接点のx座標は、aの値によらないのがポイントになります

つまり、aの値を変えてみることで、二次関数曲線の形を変えてみたとしても、一次関数と接点を形成するx座標は不変ということです

このaを変える操作が、図の座標全体を支える下側の木片を傾ける操作に相当します

下側の木片が傾くと、その上にある各棒の相対的な高さが変わります

一方で、各棒のx座標は維持されます

このため、木片を傾けた結果、図示された関数はx座標上の接点を保ちながら、対応する形の変化を示すというわけです

この数学そのものは別に面白くはないんですが、このような視覚的に分かりやすい教材は感心に値しますよね

こういう工夫に感心してしまうのは、私自身、理科の塾講師の経験があり、視覚的に分かりやすい説明をするために試行錯誤していたからかもしれません（〇葉学院てとこです）

しかし、この教材は一見、作るのが大変そうですよね

実際、この作成者のツイッターを拝見すると以下のようなことが書かれています

「この教具は，教職大学院のゼミ生と教材研究していて考えたものです．私が大体の仕組みをつくって，昨日キャンパス内の屋外で，ゼミ生とふたりでやすりをかけたり，グラフを書き込んだりして仕上げました．」

いろいろと手が込んでいますね．．．

しかしです

仕組みをつくることが一番重要な段階ですから、GAINENZの立場としては、その後のやすりがけとかには時間を使いたくないと思うわけです

そこで、今回はこの仕組みをBlenderによる3Dアニメーションで再現すればええやん、となりました

以下では、この仕組みをどうやってBlenderで再現したかについて解説します

数学的背景の理解

数学的背景と偉そうに書きましたが、数学を解説する仕組みをつくるなら、まずはその数学を理解することが必要です

つまり、二次関数(y=x^2+1+ax)と一次関数(y=c|x|)がaによらず接点を形成するのは本当か？ということを数学的に確かめる必要があります

そこで、まずは普通に、これらの連立方程式を解いて接点を求めてみましょう

今回に関しては、微分とか使いますので、中学から高校程度の数学知識があればよさそうです

立式は以下の通りです

したがって、接点のx座標はたしかにcによらず、一定の値である±1になることが分かりました

グラフの概形の理解

Blenderでいきなり作図、というわけにもいきませんので、まずはエクセルでグラフの形をつくってみましょう

一番上の教材を意識して、グラフは離散的なプロットで表現することとします

ここで、x軸の取る値は-2から2までを0.1ずつとします

aの値は0と1と-1を試行しましょう

各場合のcについては、方程式の解c = 2 + a (x >= 0)かつc = -2 + a (x < 0)を用いることで、aに対応するcの値が得られます

実際に求めた値を列挙すると下の通りです

a = 0のとき、c = 2 (x >= 0)かつc = -2 (x < 0)

a = 1のとき、c = 3 (x >= 0)かつc = -1 (x < 0)

a = -1のとき、c = 1 (x >= 0)かつc = -3 (x < 0)

これらの値をベースに、二次関数と一次関数を描いてみた結果が下の通りです

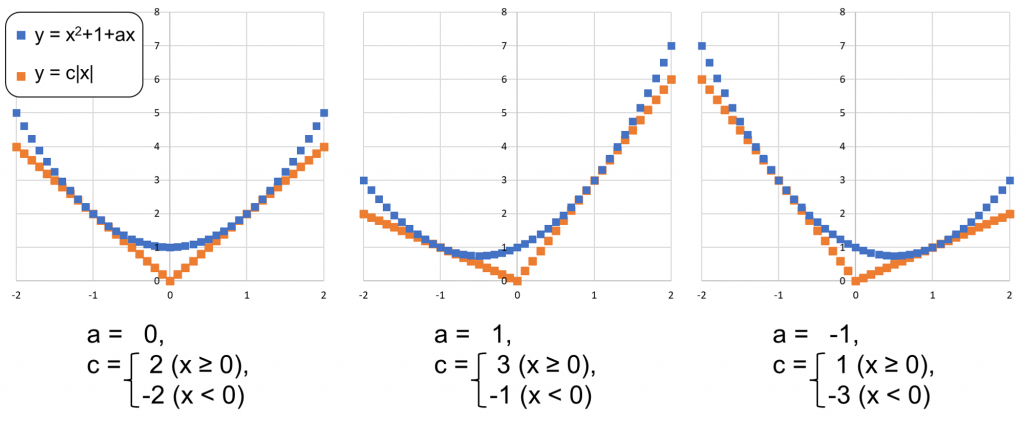
きれいな結果ですね

当たり前ですが、接点は必ずx=±1に見られます

Blenderによる教材の再現

エクセルの図をBlenderで表現してみましょう

まずは、エクセルの図を画像形式にしてBlender上に出現させます（下）

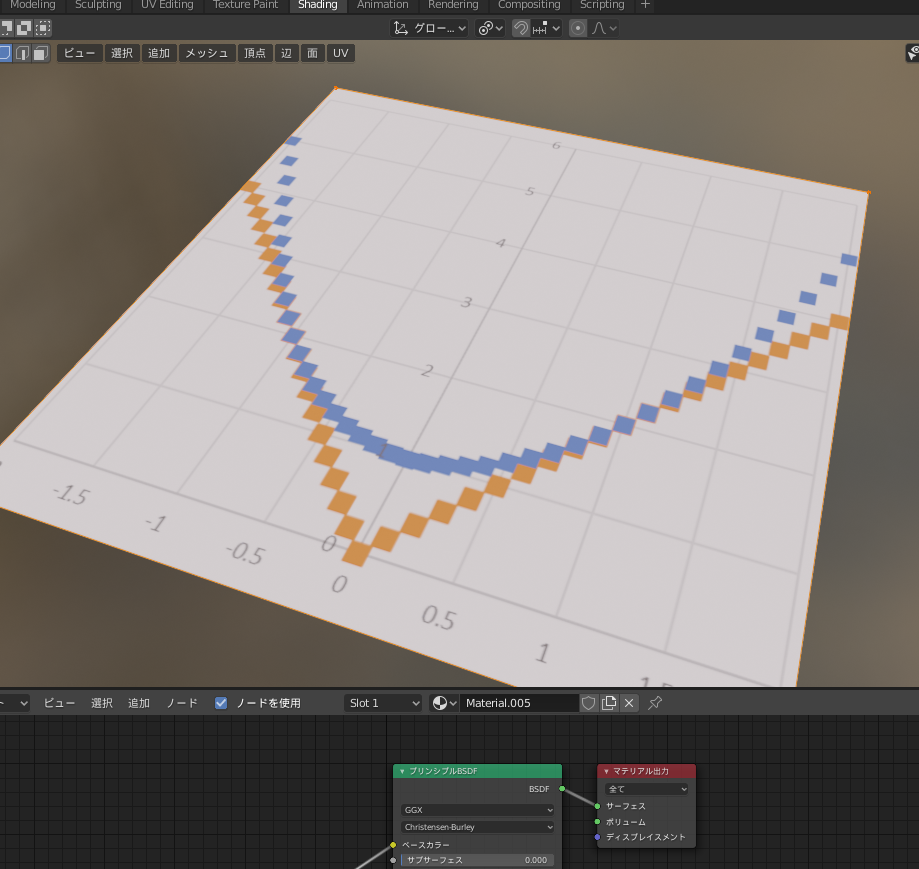
ここまでできたら、画像の各点に対応する箇所に、頂点をつくるだけです

Ctrl+Rで横軸を分割してから、縦軸を細分化するとよいでしょう

ミラーモディファイアを使うと、作業を効率化することができます

テキトーでもいいので頂点をつくりたいという場合は、ナイフツール（Kキー）で十分かもしれません

続いては、4つの頂点に囲まれた四角形部分のマテリアル設定を行って、色を変えることで、プロットとして表現します

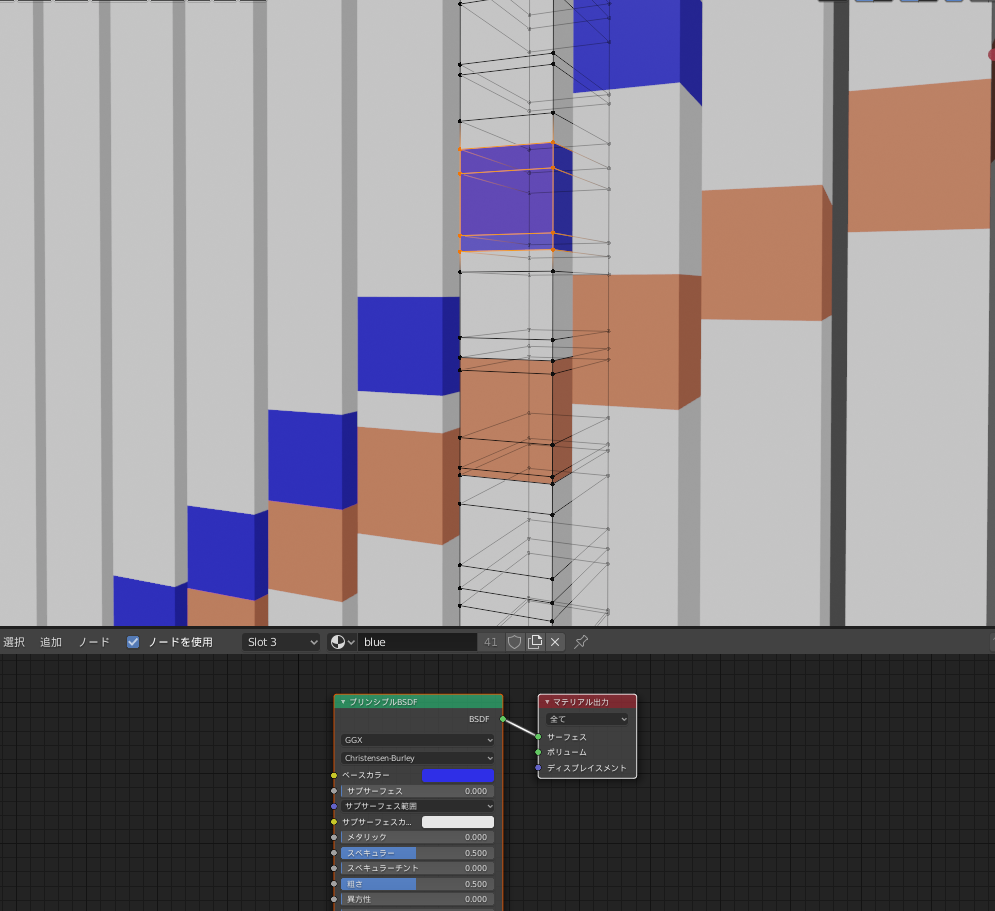
図を見ると、プロットの解像度以上に辺が分割されすぎな気もしますが、細かいことは気にしない

最後に、アニメーションをつくるため、各棒にアーマチュアを導入しましょう

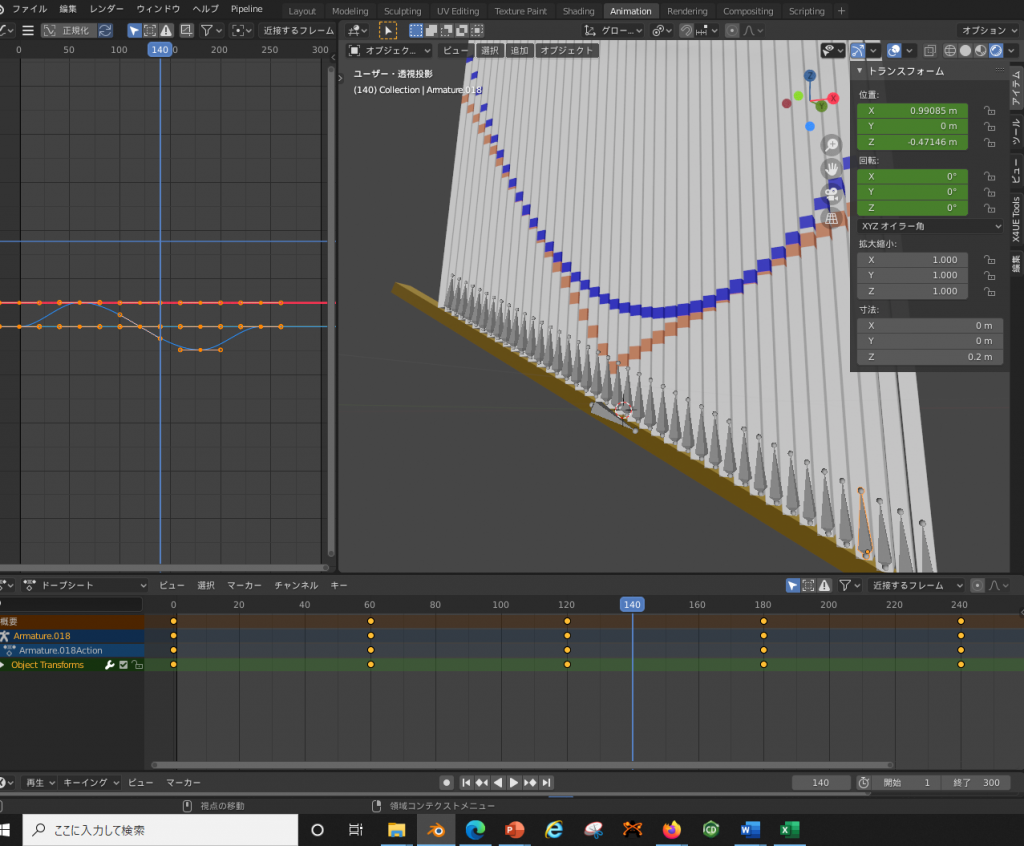
アーマチュアを41本導入しました

数自体は多いですが、その動作は図の左側に示されているように、sinカーブ的な単純なアニメーションなので余裕ですね

できたアニメーションはこちらの通りです

Blenderならではの利点としては、そもそも木材を用意する必要がないとか、やすりがけをする必要がないとかだけでなく、aがどのように変化しているかも連動して示せるということが挙げられます

まあ、手に取れる教材のほうが優れている部分ももちろんあると思います

今回はたまたま見つけた数学教材を題材として取り上げましたが、数学に限らず他の教材でも使えそうです

以上、Blenderで数学教材を再現する方法でした

12/12追記

Processingを用いることで、本教材のグレードアップを試みました

具体的には、クリックによる傾き調節が可能な教材として仕上げました

こちらからご覧になれます