共重合反応の確率シミュレーション（結果・考察編）

３．シミュレーションの視覚化と結果・考察

　アルゴリズム編に記載したプログラムをR Studioで実行することで、様々なBの割合においてAがBABに変換される割合、すなわち確率をシミュレーションした。

　設定したプログラムによって適切にシミュレーションが進行することについては、print()関数で確かめることができた。入力内容と出力結果のそれぞれの一部を図7に示した。図7aでは、初期の反応容器内にある分子として3つのＡと6つのBを定義している。その結果、一段階目の反応においては、6番目のBと2番目のAが選択されることでBAが生成され、flaskの最後尾に追加されることが確認できた(図7b上段)。

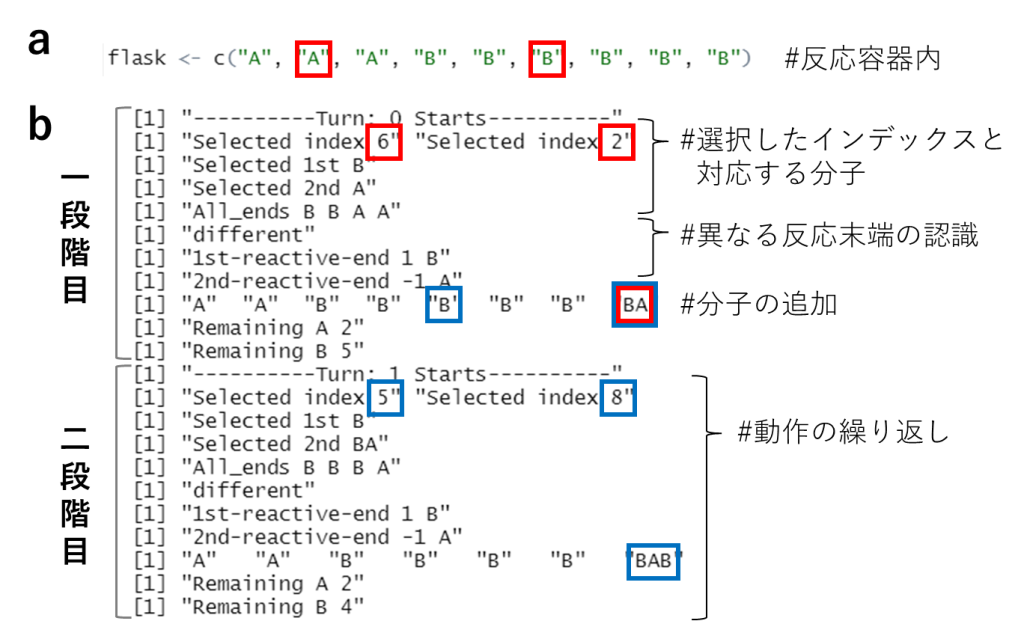
さらに、二段階目では5番目のBと8番目となったBAが選択され、生成したBABが追加されることが確認できた(図7b下段)。したがって、記述したプログラムが適切に動作していることが確認できた。

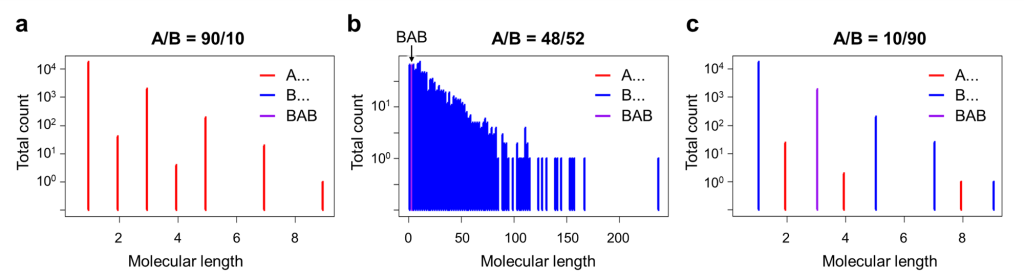
　続いては分子の総数を増やし、より現実的なシミュレーションを行った。実際の化学反応において分子は1 mol (10²⁴個)程度存在するが、計算を終了させるため、分子の総数は5000個とした。反応開始時点でのBの割合を0.1、0.52、0.9とした場合に、最終的に生成した分子(文字)の長さに対する分布を図8に示した。図8では、Aから始まる分子(A…)は赤、Bから始まる分子(B…)は青、BABは紫の実線で表示している。図8aより、Bの割合が0.1と低い場合、生成物の長さは比較的短く、かつBABを生じていないことが分かる。これは、無作為抽出によってAが選ばれやすく、分子の両端に対して連続的にAが結合する確率が高かったためであると考えられる。図8bより、Bの割合が0.52の場合は、わずかにBABを生じるものの、それよりも長い分子を数多く生じていることが分かる。これは、AとBの数が同程度であることによって、どちらも無作為抽出で選ばれやすく、ABABAB…と分子が交互に伸長する確率が高くなったためであると考えられる。図8cより、Bの割合が0.9と高い場合は、生成物としてはBABを最も生じていることが分かる。これは図8aのAがBに置き換わった場合に相当しており、分子の両端が連続的にBと衝突する確率が高いことで、生成したBABはそれ以降の反応を起こしにくかったためであると考えられる。

　様々なBの割合に対して、反応したAのうちBABとなったものの割合を実験的に得られた確率値として図9に示した。図9aに着目すると、Bの割合が0.5以下である場合には、全くBABを生じないことが分かる。一方、Bの割合が0.5以上となると、BABを生じる割合が単調に増加することが明らかとなった。特に、Bの割合が0.96、0.98である場合には、BABの生成確率がそれぞれ約85%、約90%となった。したがって、Bの割合を最小限にしつつもBABの生成効率を高めるには、Bの割合が少なくとも0.96から0.98程度必要であることを明らかにできた。

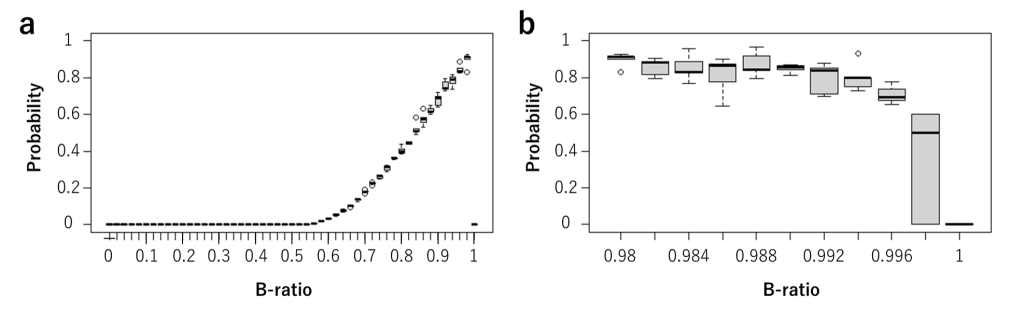
　興味深いことに、図9bより、Bの割合が0.98以上となる場合は、Bの割合を高めてもBABの生成確率が増大しにくくなることが分かった。これは、Bの割合が高すぎる場合には、B同士が選ばれてしまう状況が長く続き、未反応状態が続くことを抑制するwhile文によって反応が止められてしまったためであると考えられる。すなわち、AやABが存在しているにも関わらず、BABを生成する前に反応が止まってしまったため、0.998という高いBの割合であってもBABの生成確率が0となるようなケースを生じたと考えられる。このような挙動は現実の化学反応では起きず、無作為抽出を用いたシミュレーションならではのものである。現状として、計算速度を短縮させるために未反応状態の上限を1000回と設定しているため、この上限を増やすことで、さらに現実に近いシミュレーションを実現することができる。

４．結論

　本記事では、分子A,Bが交互に伸長する反応のシミュレーションを行うことで、AとBの比によって異なるBABの生成確率を系統的に調査した。その結果、Bの割合が高いほどBABの生成確率が高くなるという、現実に見られる傾向を再現することができた。特に、少ないBであっても高い確率でBABを得るには、Bの割合が96から98%程度必要であることが分かった。これによって、莫大な数の化学実験を行わずに、最適なBの割合を明らかにすることができた。