フーリエ変換を体験せよ

フーリエ変換って聞いたことありますか？

理系であれば、少なくとも聞いたことはあるのではないでしょうか

簡単に説明します

一言でいうと、重なり合ってしまった波形を、元の波形の形に戻す作業のことです

例えば、典型的な波として、音波を思い浮かべてみてください

音は、波の振動数が高いほど、高い音として聞こえ、振動数が低いほど、低い音として聞こえます

ですので、ドレミファソラシドのいずれかを用いて表現するならば、ファの方がミより高い振動数をもっています

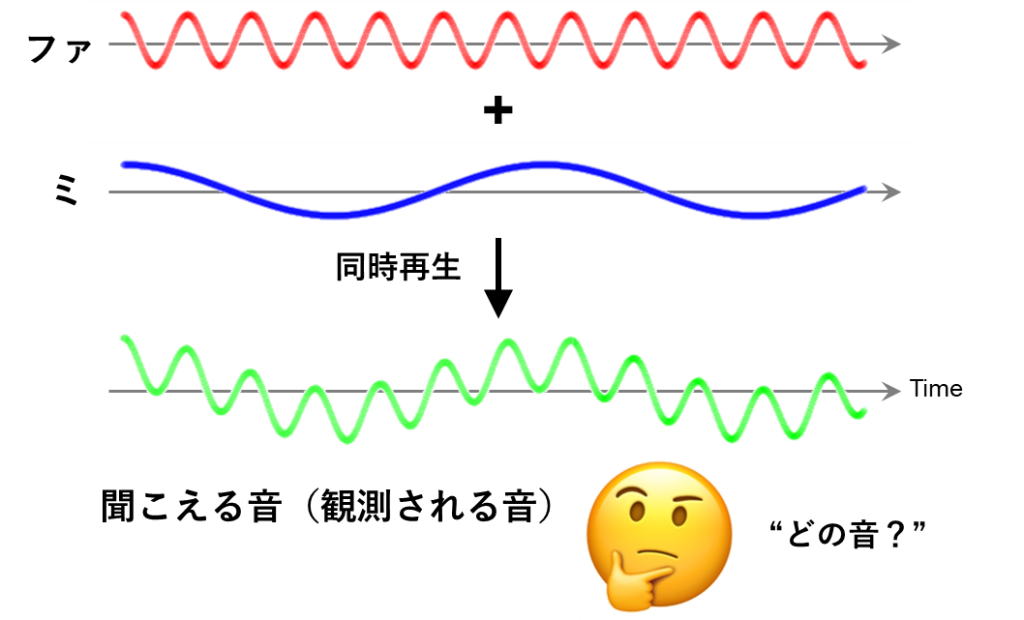
これをやや大げさに表現したものが下の図です

それぞれは単純な波形で表すことができますので、音楽の成績が優秀だった人は、どちらがどの音であるか、聞けば分かるかと思います

しかし一般的には、我々の耳に入る音というのは、そう単純ではありません

もしかしたら、ファとミが同時に再生されていて、その重なり合った波（図の緑色）が我々の耳やマイクに伝わってきているかもしれません

こうなると、どの周波数（振動数）の波が再生されているか、人間の力では検知しにくくなってきます

この問題を解決するのが、フーリエ変換です

つまり、観測された音から、どのような周波数の音が入っているかを明らかにする技術をフーリエ変換といいます

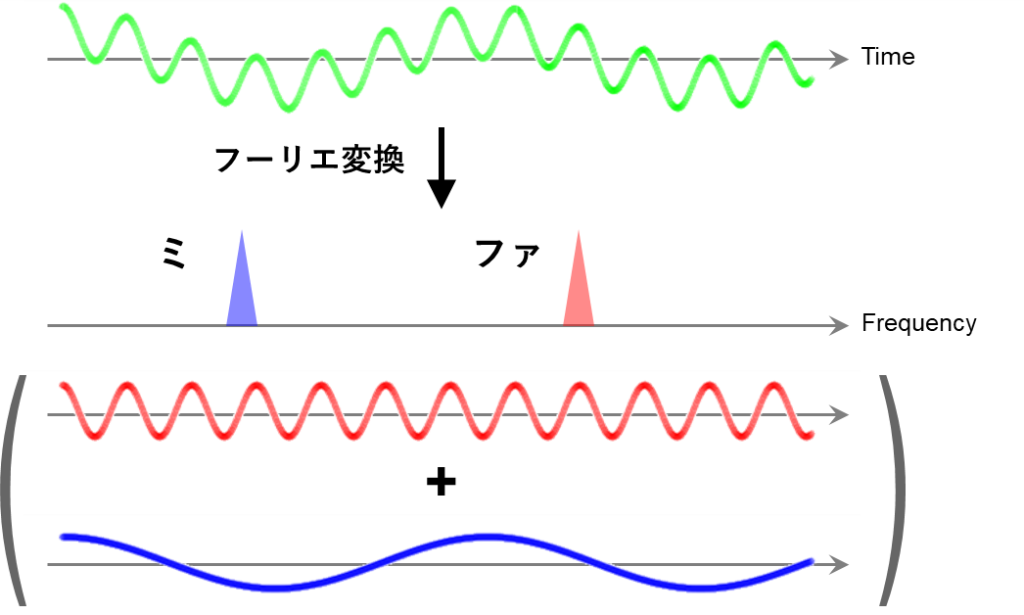
具体的なイメージは下図の通りです

緑色の波はミとファの重なりであるため、時間を横軸としたとき、その振幅はもはや単純なsin関数では描けない形となっています

ここで、この緑色の波に対してフーリエ変換を行うと、ミの音に対応する周波数と、ファの音に対応する周波数がピークとなって現れます

これによって、緑色の波は、それぞれの周波数をもった波の重なり（合成波）であることを明らかにできます

Processingで体験しよう

というわけで便利なフーリエ変換なのですが、その数学を理解しようとすると難しく感じられる方も多いと思います

そこで、視覚的にフーリエ変換を理解できることが望ましいと考えまして、画像処理の力を借りることにしました

以下のページから、「波を合成する過程」と「その周波数を明らかにする過程」を実際に遊んでみることができます

フーリエ変換体験器

以下は、表示画面の説明です

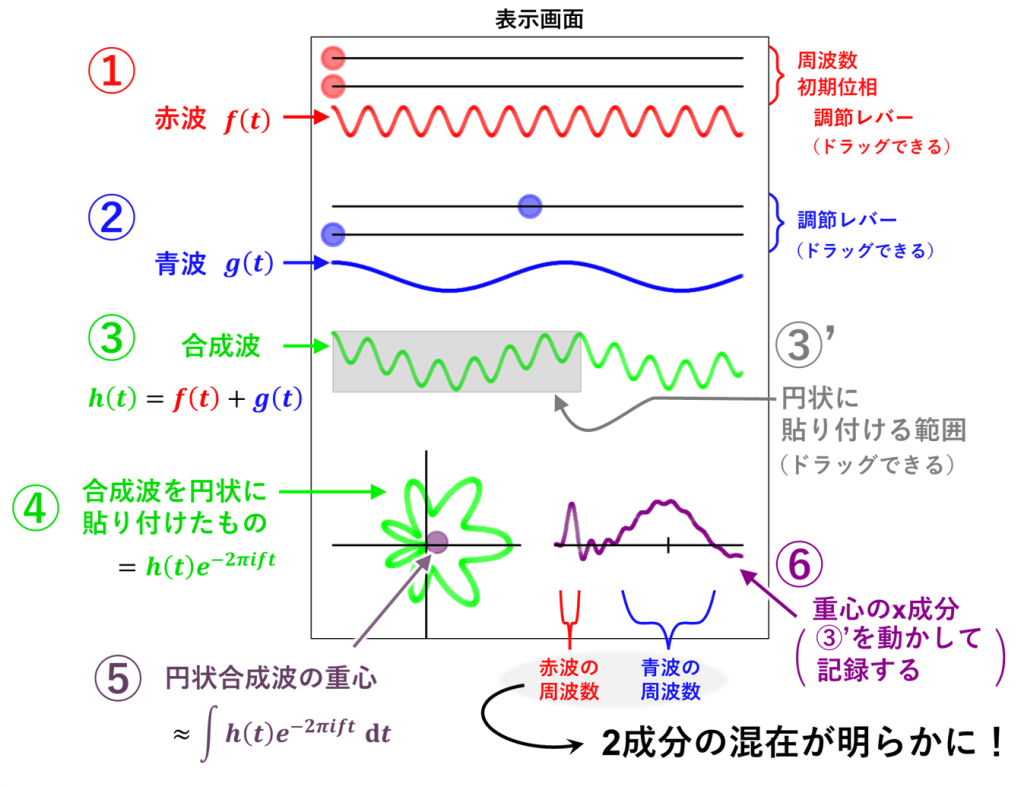
①2つある構成波のうちの1つ目である赤波のパラメータを調節できます。具体的には、その周波数と初期位相をいじることができます。赤丸をドラッグして、適当な位置に設定してください。（初期位相はノリで弄れるようにしましたが、最初の設定のままにしておくことをオススメします）

②2つある構成波のうちの2つ目である青波のパラメータを調節できます。

③上記の①と②で設定した波の合成波が表示されます。

③’ 続いては合成波を円状に貼り付ける作業が必要となります。その範囲をドラッグによって指定してください。

④指定された範囲の合成波が円状に貼り付けられます。

⑤円状に貼り付けられた波の重心位置が表示されます。

⑥上記⑤において表示された重心のx座標がプロットされます。③’の貼り付け範囲を動かしてみることによって、どのようなプロットが現れるかを楽しんでください。もし合成波が、純粋に1つの周波数をもつ波によって構成されているのであれば、現れるピークは一つになると思います。一方、合成波において異なる2つの周波数が混在しているのであれば、現れるピークは二つになると思います。

【参考資料】

今回のプログラムを作製するにあたって、3Blue1Brownさんの動画を参考にしました

プログラムそのものは完全なオリジナルですが、円状に巻き付けた合成波の重心を計算するという考え方は、動画を見るまでは知りませんでした

本ページでは解説しきれなかった点について、この動画では完全に説明していますので、もし興味があれば御覧ください