k-近傍法(k-nearest neighbor algorithm, k-NN)という分類法があります。
与えられた任意のデータが、どのクラスに属するのかを決定する手法です。
クラスというのは例えば、花の種類とかです。
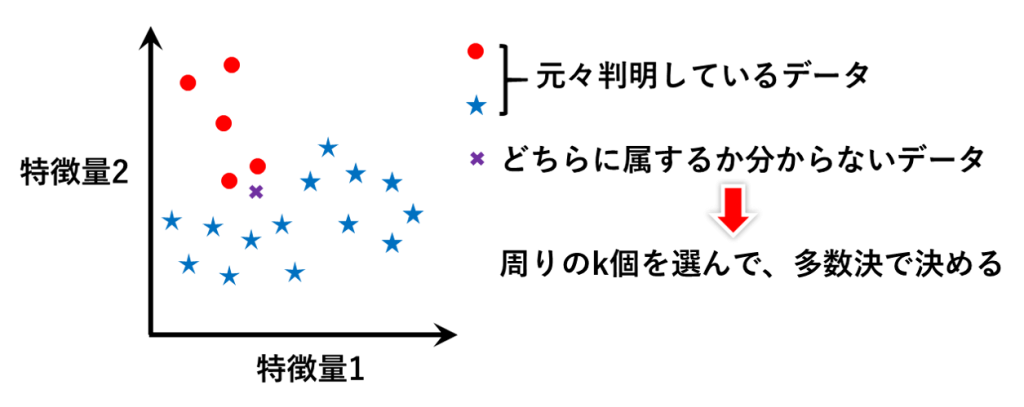
例えば図のようなデータがあったとします。ある特徴量1,2をもつ花は●なのか★なのかを分類したという、既知のデータです。
ここで、新たに✖というデータが入ってきたとき、✖は●なのか★なのかを決めたい、みたいな状況で有用な手法です。
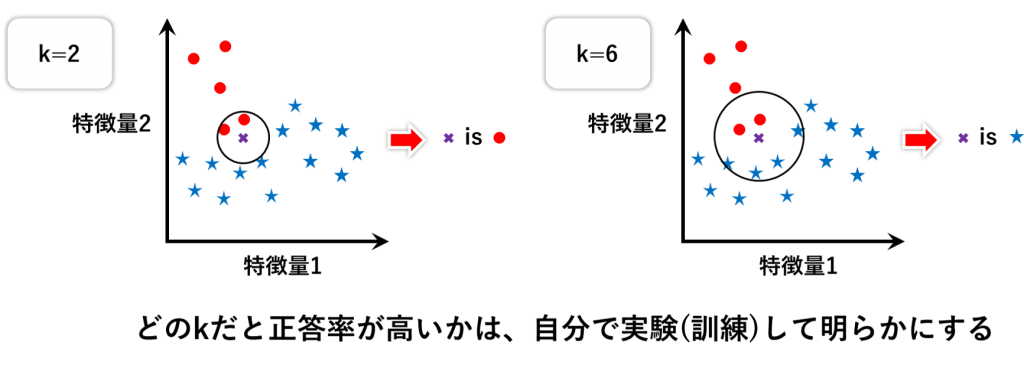
もしk=2とするなら、2個の近傍法ということになるので、周りの2個を選んで、それと同じにしてしまおうというアルゴリズムになります。
この場合は、選ばれた2個が●なので、✖も●だろうということになります。
別パターンとして、もしk=6とするなら、★のほうが●より多く選ばれるので、✖は★だろうという多数決になります。
そういうわけで、kの値によって✖がどうなるのかは色々ありえます。
でも✖はどっちかしかないわけですから、これだと困りますよね。
ということで、どのkだと正答率が高いかは、自分で実験して明らかにするしかありません。
具体的には、実験とは訓練とテストのことを指します。
今あるデータから、kを自分で決めてみるということを訓練といいます。
そして、そのkが合っているかを確かめる作業をテストといいます。
訓練とテストを自分で行うということです。
正答率を出すためには、テストの解答は既に分かっているものを利用しないといけません。

ここでは、irisという、花の特徴量とクラスが予め判明しているデータフレームを使います。
このデータフレームはRで利用できるようになっていたと思います。R Studioというソフトを使うと便利です。
これを活用して、irisのデータフレーム(trainA)中のランダムな数行(testB)のクラスを最適なkで予測する関数k_optimizeをつくってみましょう。
コードの書き方
k_optimizeという関数の中身を説明します。
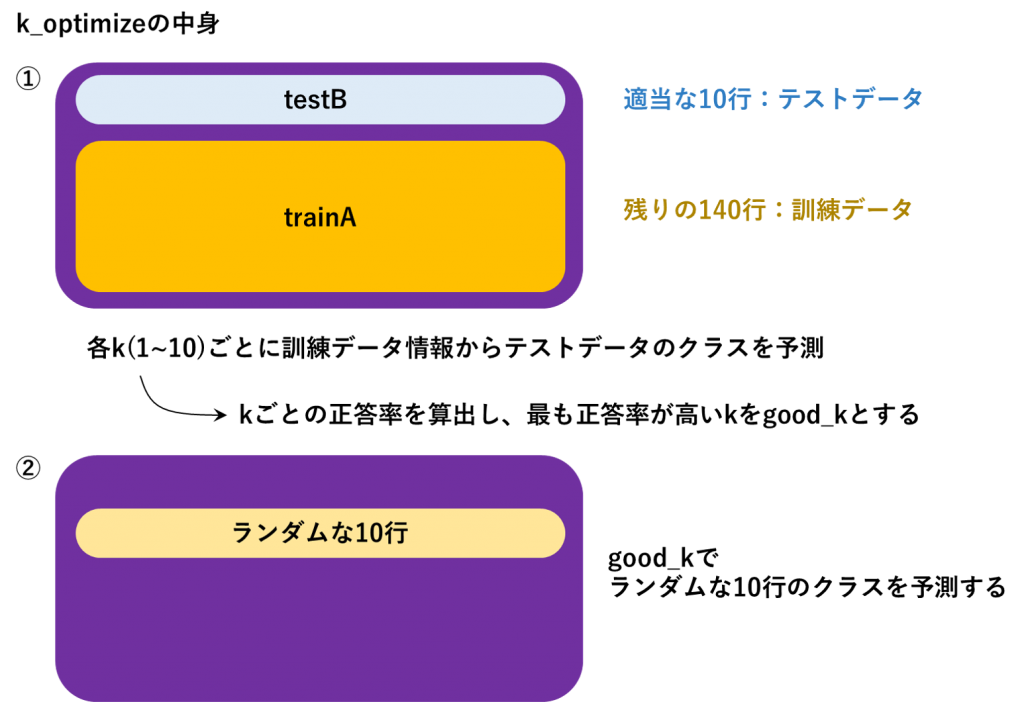
①まず、dataという名前にirisというデータフレームを代入したとします。
data(図では紫)は訓練データとテストデータに分ける必要があります。
そこで、10行だけをテストデータ(AnoTest)として選び、残りを訓練データ(AnoTrain)にします。
続いて、例えば、k=1として、訓練データ情報からテストデータのクラスを予測してみます。
これはRのパッケージであるknn()という関数が勝手にやってくれます。
knn(訓練データ、テストデータ、訓練データの正答クラス、k)という感じで書き、kekkaというオブジェクトに代入しておきましょう。
kekkaの内容は、テストデータの予測になります。
AnoTrainから得た情報で、AnoTestのクラス(花の情報)を予測してくれます。
kekkaが、元々分かっているテストデータのクラスとどれだけ合っているかは
kekka == AnoTest[,5]で判明します(5列目を選んでいるのは、5列目にクラスが入っているためです)。
10行テストしていますから、TRUE FALSE TRUE TURE…というように10個分の評価が返ってくるはずです。
TRUEは1で、FALSEは0ですから、sum()で合計すると、正答数になります。これを、length(AnoTest[,5)で割れば正答率です。
kが1のとき、この作業を終えたら、次にk=2, 3, 4…10と続くようにしておきます。
そういうわけで、for文を先頭に用意しておくのです。
それぞれのkの場合での正答率を記録しておく用のベクトルをつくっておかなければなりませんから、それは初めにseikai_counterとして用意しておきます。
for文の処理が終わる直前ごとに、seikai_counterの中身は正答率で置き換えるようにしておけばいいのです。
すると、kが10まで終わったころには、seikai_counterの中には全てのkについての正答率が記録されていますから、どのkのときが一番正答率が高かったかが分かります。
ということで、which.max()関数で、seikai_counterの中からインデックスをとってくれば、正答率の最も高いときのkの値をとってくることができます(インデックスがk=1,2,3…に対応しています)。
これはgood_kという名前にしておきます。
②good_kが決まったので、それをkとした場合の予測を行います。
受け取る引数は、訓練データ(trainA)とテストデータ(testB)です。
その結果、どれくらい合っているかは論理記号==で分かります。
以上をまとめますと、以下のようなコードになります。
k_optimize <- function(trainA, testB){
AnoID <- sample(nrow(trainA), 10)
AnoTest <- trainA[AnoID,]
AnoTrain <- trainA[-AnoID,]
seikai_counter <- rep(0,10) #各kの場合の正答率を格納するベクトル
for(k in 1:10){
kekka <- knn(AnoTrain[,-5], AnoTest[,-5], AnoTrain[,5], k)
print(kekka == AnoTest[,5]) #予測と実際がどれだけ合っているかを表示
print(sum(kekka == AnoTest[,5])/length(AnoTest[,5])) #正答率
seikai_counter[k] <- sum(kekka == AnoTest[,5])/length(AnoTest[,5])
}
good_k <- which.max(seikai_counter) #最も高い正答率のインデックスがkに対応
print(“good_k is”)
print(good_k)
final_result <- knn(trainA[,-5], testB[,-5], trainA[,5], good_k)
print(“showing result”)
return(final_result == testB[,5]) #最終的な予測と実際がどれだけ合っているかの表示
}
data <- iris
k_optimize(data, data[sample(nrow(data), 10),])
この場合、trainAを「irisの入ったdata」とし、testBを「trainAのランダムな10行」にしています。
実行してみると、例えば下のような応答が返ってきます。

k=1~10のそれぞれの場合の正答率が表示されていますが、k=4のとき最高の1 (100%)となっています。
このkをgood_kとして、dataが訓練データ、dataのランダムな10行がテストデータとなった場合の予測結果を表示させると、全てTRUEになったというわけです。
めでたし。
世界一わかりやすいk-近傍法のやり方でした。









コメントを残す
コメントを投稿するにはログインしてください。