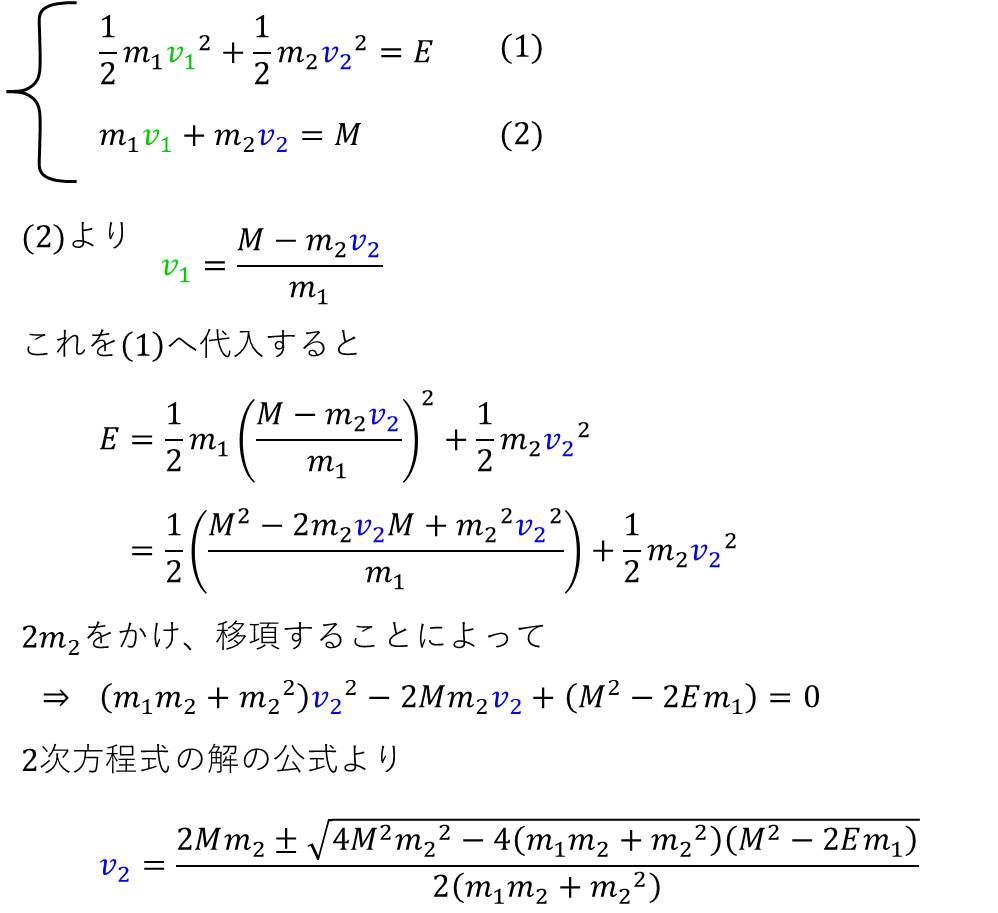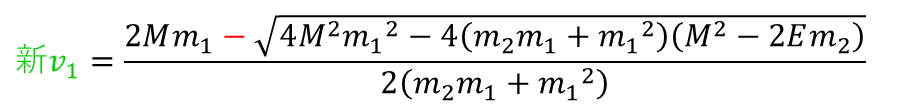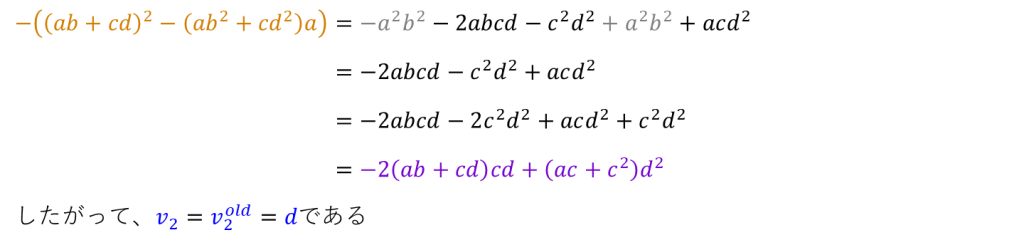質量1 kgの物体1に質量100n kgの物体2をぶつけると、物体1の衝突数は31415…と円周率の10n倍になります
これについては、下のページからシミュレーションすることができます
初期設定では、1 kgの物体に100 kgの物体をぶつけることになっており、衝突数は31となるはずです(円周率の最初の2桁です)
これは動画ではなくProcessingを用いてプログラムされたものです
ですので、質量と速度を変えることもできます
一番上の+ボタンと-ボタンから自由にその値を変えて、試してみてください
FirefoxとiPhoneのSafariでは動作確認済みです
Microsoft Edgeではボタンの位置が正常でなく、本来の位置より上側になっていますので、そこを探してください
あと、質量を10000 kgとする場合は物体のすり抜けバグが起きてしまいますが、見た目以外には問題がないため、ちゃんと314と出るはずです
今回は、本プログラムを作成するためのアルゴリズムの本質部分を解説します
画像処理を用いたシミュレーション方法
画像処理の方法として、今回はProcessingを用います
ですので、javaで書いていくことになります
if文くらいしか使わないので、全体的な書き方は他の言語とそれほど変わらないです
命令時に毎回、文末にセミコロンがつくくらいでしょうか
①変数定義
前回の記事では、この衝突の物理について解説しました
今回のアルゴリズムは、これに比べたらかなり簡単です
なぜなら、今回のアルゴリズムは「物体がぶつかったら、速度を更新し、衝突数を数える」だけだからです
では、今回のプログラムで用いる変数のうち、重要なものを下に示します
javaで書きますから、float (変数名);という表記で定義します
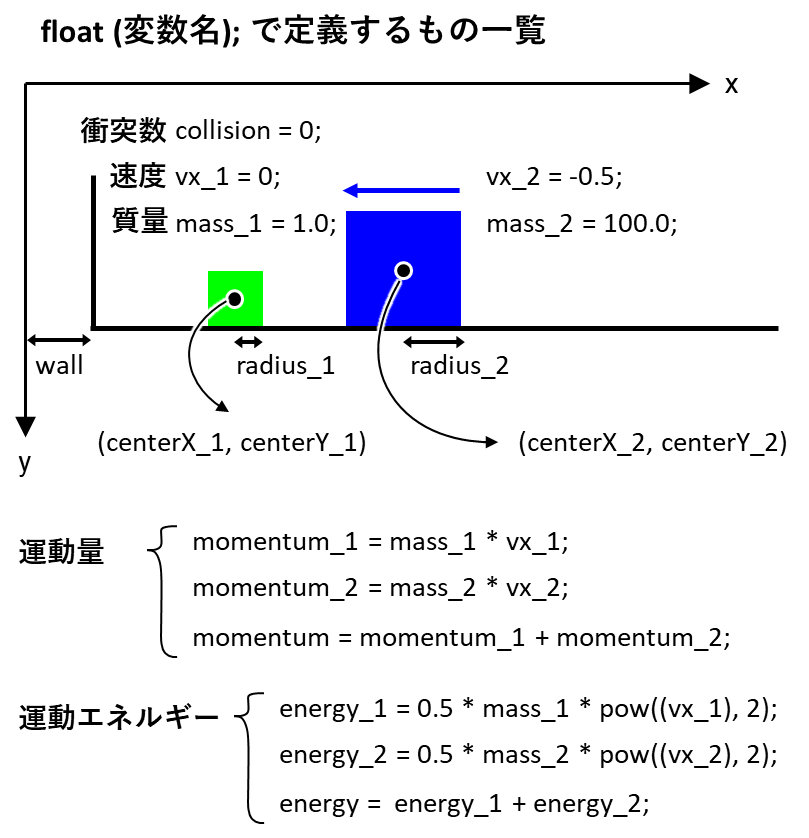
上から順に説明すると、まずは衝突数がcollisionです。初期値は0
物体nの速度と質量はそれぞれ、vx_nとmass_nとして定義します
壁のx座標はwallとします
そして物体nの中心のx,y座標は、centerX_nとcenterY_nとして定義します
今回の物体は正方形ですが、幅の半分の値をradius_nとしておきましょう
これで基本的な値は出そろいました
あとは運動量と運動エネルギーが重要な物理量となりますから、これらも物体nについて、momentum_nとenergy_nとして定義しておきましょう
物体1と2の合計の運動量・運動エネルギーはそれぞれ、momentum・energyで表しています
以上が、今回のプログラムに登場する重要な変数たちです
②アルゴリズム
ここからが、本題のアルゴリズムです
プログラムする内容は、主要な部分に限れば、実は下の図の内容だけです
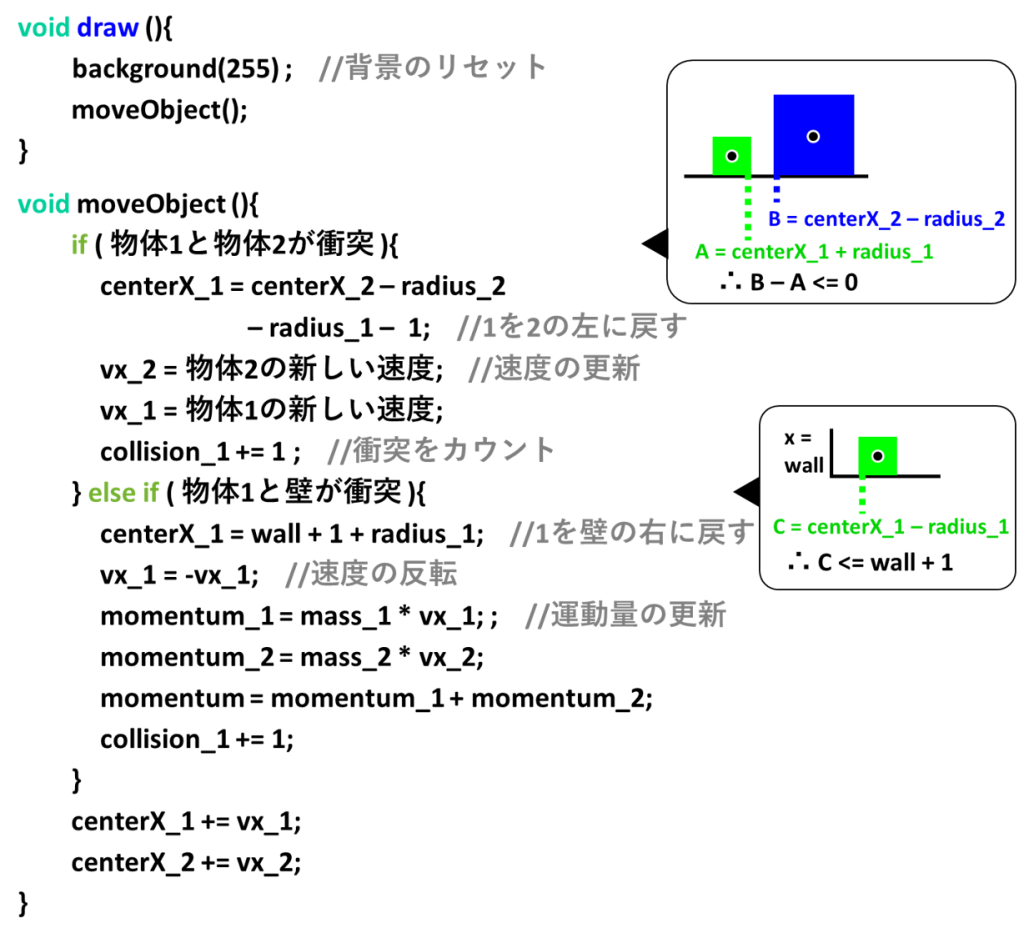
順に解説します
このプログラムは2つのブロックに分けることができます
void draw() 部分とvoid moveObject() 部分です
void draw() 部分では、毎回背景を白にしてリセットした後、moveObject()の演算に基づいた描画を行っています
そこで、肝心になってくるのが、moveObject() の内容です
moveObject() はその名の通り、物体を動かす演算を行っています
すなわちmoveObject()では、物体nのx座標であるcenterX_nを、毎回vx_nの値だけプラスすることによって、物体の位置を変動させています(上図の下から2・3行目)
ただし、moveObject() から始まって、最後のcenterX_nの書き換えに至るまでには、if文とelse if文があることが確認できますよね
実はこのifとelse ifが、①「物体1と物体2が衝突した場合」と②「物体1と壁が衝突した場合」のそれぞれに対応しています
①if文の中身
図の、最初のif文の中身をご覧ください
このif文には、「もしも2つの物体が衝突したら、それらの速度を更新する」という内容を書きます
このため、ifの条件記述欄であるカッコ( )の中身には、物体の衝突条件を指定することになります
ここで、物体2の左先端を表すx座標を「B = centerX_2 – radius_2」と表し、物体1の右先端を表すx座標を「A = centerX_+1 + radius_2」と表したとしましょう
AとBを使って衝突条件を表すとすれば、「物体2の左先端Bを物体1の右先端Aが超えた時」が衝突の起きた時となります
したがって、「B < A」が物体1と2の衝突条件となります
代わりに、「B – A < 0」と書いてもいいです
衝突後に起きる事象については、中カッコ{ }の中に書きます
具体的には、物体1の位置の補正とvx_2とvx_1の更新です
速度が速すぎると物体1が物体2に食い込んでしまい、衝突数がおかしなことになってしまうので、「centerX_1 = centerX_2 – radius_2 – radius_1 – 1」として、物体1を物体2の左側に戻してあげます
速度を更新するための具体的な値(文字式)については、本記事の一番下で解説します
最後に、collisionをプラス1することによって、衝突数を数えましょう
これだけです
②else if文の中身
物体1と壁が衝突するときの条件を、else if文のカッコ( )の中に書きましょう
ここで、壁のx座標はwallであり、物体1の左先端のx座標は「C = centerX_1 – radius_1」です
よって、C <= wall + 1が、物体1と壁との衝突時を表す条件となります
1はノリでつけたので、なくてもよさそうです
衝突後の事象は、中カッコ{ }の中に書きます
物体1が壁に食い込むことがあるので、「centerX_1 = wall + 1 + radius_1;」として、物体1を壁の右側に戻しておきましょう
衝突後は、速度の更新も行います
弾性衝突ですから、新しく更新される速度は、衝突前の速度が正負反転したものとなります
ですので、vx_1 = -vx_1という代入を行います
さらには、運動量合計値の更新も行います
①のif文では更新しなかったのに、なぜ②のelse if文では更新するのでしょうか
それは、①の場合では合計値が変わらない一方、②の場合では合計値が変わるためです
運動量保存の法則は、物体1と物体2の衝突時のみ保持されるからですね
というわけで、「monemtum_n = mass_n * vx_n;」として、物体nの運動量を更新しましょう
その合計値は「momentum = momentum_1 + momentum_2;」で更新できます
これが書き終わったら、最後にcollision_1 += 1;として衝突数を数えるだけです
以上が、「衝突の物理シミュレーションによって円周率を求める方法」の全容です
【補足】更新する速度の具体的な文字式
上の①の「物体1, 2が衝突する」という場合の解説では、衝突が起きた後の速度を表す文字式について省略しました
これは今回のアルゴリズム編では、あまり本質的ではないためです
しかし、物理の観点からすると本質的です
よって、補足事項としてこれらを求めることにします
考える式は2つだけです
運動エネルギー(E)保存の法則と、運動量(M)保存の法則です
この2つを連立方程式として、未知の値である2つの速度v1・v2を求めます
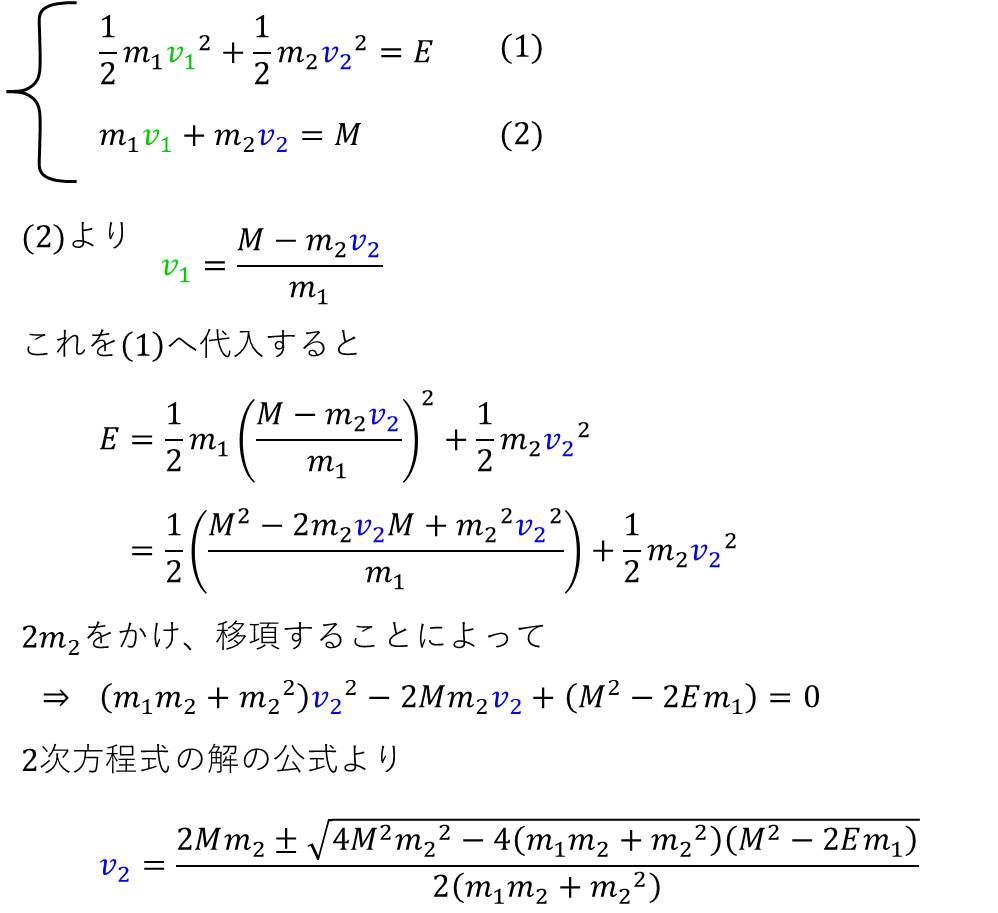
まずは上図のようにv2が求められるはずです
ただし、2次方程式の解ですから、2つの解が求まっています
新しい速度は、このどちらなのでしょうか?
前回の物理編を見ていれば、簡単に答えられます
正解は、大きい方が新しい速度の解です
この理由は、下の画像の通りで、運動エネルギー保存の法則を表す円と運動量保存の法則を表す直線の交点が解となっており、この交点は軸の上側へ必ず上昇していくためです
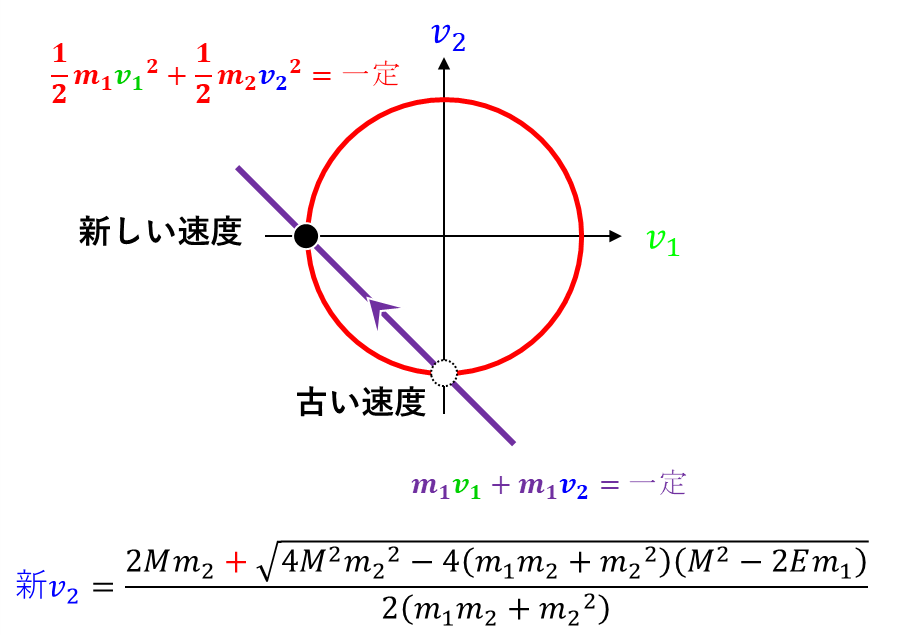
言い換えれば、物体2は毎回、左側から右側に向かう衝突を受けることになるので、確実に右側への速度を増加させます
v1の解についても、同様の手順で求めることができます
運動エネルギーと運動量の式においてv1とv2は交換可能なので、v2の解に含まれるm1をm2に、かつm2をm1に変えれば終了です
ただし、新しいv1は2つある解のうちの小さい方となります
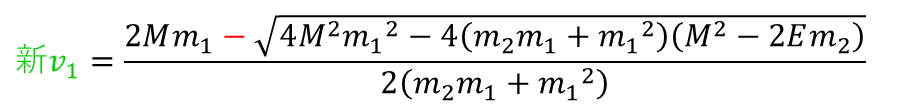
これは、物体1と2の衝突時は、1は必ず左への速度を増大させる(マイナス側へ大きくなる)ためです
したがって、衝突時のif文において、これらの新しい速度で物体の速度を更新すれば、衝突を画像処理で再現することができます
以上で、アルゴリズム編は終了となります
読んでくださりありがとうございました。
【補足の補足】速度v2の解の小さい方が古い方の速度であることの証明
本内容を理解する上で、正直これ以降の内容は読まなくていいです
上では、速度v2の解のうちの衝突後の方は、大きい方であることを定性的に示しました
これは文字式によって厳密に示すこともできます
ただしこの場合は、大きい方が新しい方であることよりも、小さい方が古い方であることを証明するのが楽です
以下の画像にて、それを示しました
参考になれば嬉しいです

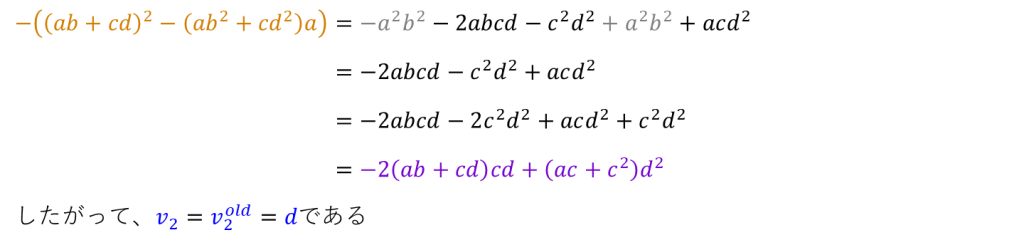
![[1]Rotaxane](https://gainenz.com/wp/wp-content/uploads/2021/09/thumbnail.png)